题目内容
14.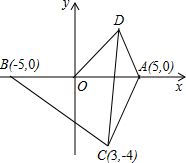 如图,在平面直角坐标系中,点A为(5,0),点B为(-5,0),点C为(3,-4),点D为第一象限上的一个动点,且OD=5.
如图,在平面直角坐标系中,点A为(5,0),点B为(-5,0),点C为(3,-4),点D为第一象限上的一个动点,且OD=5.①∠ACB=90度;
②若∠AOD=50°,则∠ACD=25度.
分析 ①利用勾股定理结合A、B、C三点坐标可得BC、AB、AC的长,再利用勾股定理逆定理可证出∠ACB=90°;
②首先连接OC,利用勾股定理计算出CO的长,进而可得B、C、D都在以O为圆心,半径为5的圆上,再根据圆周角定理可得∠ACD的度数.
解答 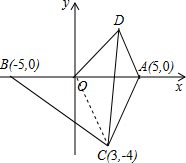 解:①∵点A为(5,0),点B为(-5,0),点C为(3,-4),
解:①∵点A为(5,0),点B为(-5,0),点C为(3,-4),
∴AB=10,BC=$\sqrt{{8}^{2}+{4}^{2}}$=$\sqrt{80}$=4$\sqrt{5}$,AC=$\sqrt{{2}^{2}+{4}^{2}}$=$\sqrt{20}$=2$\sqrt{5}$,
∵(4$\sqrt{5}$)2+(2$\sqrt{5}$)2=102,
∴BC2+AC2=AB2,
∴∠ACB=90°,
故答案为:90;
②连接OC,
∵点C为(3,-4),
∴CO=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵OD=5,
∴B、C、D都在以O为圆心,半径为5的圆上,
∵∠AOD=50°,
∴∠ACD=25°,
故答案为:25°.
点评 此题主要考查了勾股定理逆定理,以及圆周角定理,关键是掌握如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.如图,给出线段a、h,作等腰三角形ABC,使AB=AC=a,BC边上的高AD=h.张红的作法是:(1)作线段AD=h;(2)作线段AD的垂线MN;(3)以点A为圆心,a为半径作弧,与MN分别交于点B、C;(4)连接AB、AC、△ABC为所求作的等腰三角形.上述作法的四个步骤中,你认为有错误的一步是( )
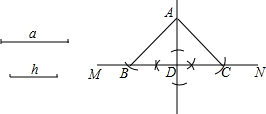
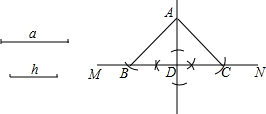
| A. | (1) | B. | (2) | C. | (3) | D. | (4) |
6. 如图是“明清影视城”的圆弧形门,这个圆弧形门所在的圆与水平地面是相切的,AB=CD=20cm,BD=200cm,且AB,CD与水平地面都是垂直的.则这个圆弧形门的最高点离地面的高度是520 cm.
如图是“明清影视城”的圆弧形门,这个圆弧形门所在的圆与水平地面是相切的,AB=CD=20cm,BD=200cm,且AB,CD与水平地面都是垂直的.则这个圆弧形门的最高点离地面的高度是520 cm.
 如图是“明清影视城”的圆弧形门,这个圆弧形门所在的圆与水平地面是相切的,AB=CD=20cm,BD=200cm,且AB,CD与水平地面都是垂直的.则这个圆弧形门的最高点离地面的高度是520 cm.
如图是“明清影视城”的圆弧形门,这个圆弧形门所在的圆与水平地面是相切的,AB=CD=20cm,BD=200cm,且AB,CD与水平地面都是垂直的.则这个圆弧形门的最高点离地面的高度是520 cm.
4.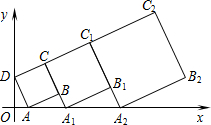 在平面直角坐标系中,第一个正方形ABCD的位置如图所示,点A的坐标为(2,0),点D的坐标为(0,4).延长CB交x轴于点A1,作第二个正方形A1B1C1C;延长C1B1交x轴于点A2,作第三个正方形A2B2C2C1,…,按这样的规律进行下去,第2016个正方形的面积为( )
在平面直角坐标系中,第一个正方形ABCD的位置如图所示,点A的坐标为(2,0),点D的坐标为(0,4).延长CB交x轴于点A1,作第二个正方形A1B1C1C;延长C1B1交x轴于点A2,作第三个正方形A2B2C2C1,…,按这样的规律进行下去,第2016个正方形的面积为( )
 在平面直角坐标系中,第一个正方形ABCD的位置如图所示,点A的坐标为(2,0),点D的坐标为(0,4).延长CB交x轴于点A1,作第二个正方形A1B1C1C;延长C1B1交x轴于点A2,作第三个正方形A2B2C2C1,…,按这样的规律进行下去,第2016个正方形的面积为( )
在平面直角坐标系中,第一个正方形ABCD的位置如图所示,点A的坐标为(2,0),点D的坐标为(0,4).延长CB交x轴于点A1,作第二个正方形A1B1C1C;延长C1B1交x轴于点A2,作第三个正方形A2B2C2C1,…,按这样的规律进行下去,第2016个正方形的面积为( )| A. | 20×($\frac{3}{2}$)4030 | B. | 20×($\frac{3}{2}$)4032 | C. | 20×($\frac{3}{2}$)2016 | D. | 20×($\frac{3}{2}$)2015 |
 如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是$\widehat{EB}$的中点,则下列结论成立的是①②③(将正确番号填入)
如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是$\widehat{EB}$的中点,则下列结论成立的是①②③(将正确番号填入)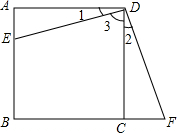 如图所示,点E是矩形ABCD的边AB上任意一点,过点D作DF⊥DE交BC的延长线于点F,DE=DF.求证:矩形ABCD是正方形.
如图所示,点E是矩形ABCD的边AB上任意一点,过点D作DF⊥DE交BC的延长线于点F,DE=DF.求证:矩形ABCD是正方形.