题目内容
19.求证:平行四边形的对角线互相平分(要求:根据题意先画出图形并写出已知、求证,再写出证明过程).分析 首先根据题意画出图形,再写出命题的已知和求证,最后通过证明三角形全等即可证明命题是正确的.
解答 已知:平行四边形ABCD的对角线AC,BD相交于点O,
求证:OA=OC,OB=OD
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠1=∠2,
在△AOD和△COB中,
$\left\{\begin{array}{l}{∠1=∠2}\\{∠AOD=∠COB}\\{AD=BC}\end{array}\right.$
∴△AOD≌△COB(AAS),
∴OA=OC,OB=OD.
点评 此题主要考查了平行四边形的性质以及全等三角形的判定和性质,解题的关键是熟记平行四边形的各种性质以及全等三角形的各种判定的各种方法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.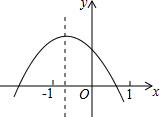 已知二次函数y=ax2+bc+c的图象如图所示,则下列结论中,正确的是( )
已知二次函数y=ax2+bc+c的图象如图所示,则下列结论中,正确的是( )
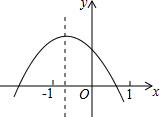 已知二次函数y=ax2+bc+c的图象如图所示,则下列结论中,正确的是( )
已知二次函数y=ax2+bc+c的图象如图所示,则下列结论中,正确的是( )| A. | a+b+c>0 | B. | b2-4ac<0 | C. | a-b+c>0 | D. | ab<0,c<0 |
7. 如图,已知⊙O的直径AB⊥CD于点E,则下列结论一定错误的是( )
如图,已知⊙O的直径AB⊥CD于点E,则下列结论一定错误的是( )
 如图,已知⊙O的直径AB⊥CD于点E,则下列结论一定错误的是( )
如图,已知⊙O的直径AB⊥CD于点E,则下列结论一定错误的是( )| A. | CE=DE | B. | AE=OE | C. | $\widehat{BC}$=$\widehat{BD}$ | D. | △OCE≌△ODE |
4. 右边几何体的俯视图是( )
右边几何体的俯视图是( )
 右边几何体的俯视图是( )
右边几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
8.下列四个数中,为无理数的是( )
| A. | $\sqrt{\frac{1}{16}}$ | B. | $\frac{1}{3}$ | C. | 0 | D. | $\root{3}{9}$ |
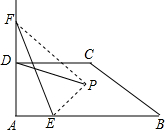 如图,四边形纸片ABCD中,AB∥CD,AD⊥AB,AB=10,AD=2$\sqrt{3}$,CD=4,点E是线段AB上的一动点,点F是射线AD上的一动点.将△AEF沿EF翻折,点A的落点记为P,连接PD.
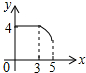
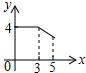
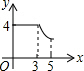
如图,四边形纸片ABCD中,AB∥CD,AD⊥AB,AB=10,AD=2$\sqrt{3}$,CD=4,点E是线段AB上的一动点,点F是射线AD上的一动点.将△AEF沿EF翻折,点A的落点记为P,连接PD.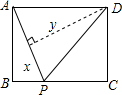 如图,矩形ABCD中,AB=3,BC=4,点P从A点出发,按A→B→C的方向在AB和BC上移动.记PA=x,点D到直线PA的距离为y,则y关于x的函数大致图象是( )
如图,矩形ABCD中,AB=3,BC=4,点P从A点出发,按A→B→C的方向在AB和BC上移动.记PA=x,点D到直线PA的距离为y,则y关于x的函数大致图象是( )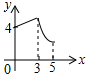
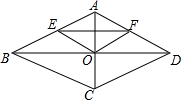 如图,菱形ABCD的对角线AC,BD相交于点O,点E,F分别是边AB,AD的中点.
如图,菱形ABCD的对角线AC,BD相交于点O,点E,F分别是边AB,AD的中点. 一张长对边平行的纸条按如图所示方法折叠,则∠1=65°.
一张长对边平行的纸条按如图所示方法折叠,则∠1=65°.