题目内容
7. 如图,已知⊙O的直径AB⊥CD于点E,则下列结论一定错误的是( )
如图,已知⊙O的直径AB⊥CD于点E,则下列结论一定错误的是( )| A. | CE=DE | B. | AE=OE | C. | $\widehat{BC}$=$\widehat{BD}$ | D. | △OCE≌△ODE |
分析 根据垂径定理得出CE=DE,弧CB=弧BD,再根据全等三角形的判定方法“AAS”即可证明△OCE≌△ODE.
解答 解:∵⊙O的直径AB⊥CD于点E,
∴CE=DE,弧CB=弧BD,
在△OCE和△ODE中,
$\left\{\begin{array}{l}{∠CEO=∠DEO=90°}\\{∠OCE=∠ODE}\\{OC=OD}\end{array}\right.$,
∴△OCE≌△ODE,
故选B
点评 本题考查了圆周角定理和垂径定理的应用,注意:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.

练习册系列答案
相关题目
18.已知关于x的一元二次方程x2+mx+n=0的两个实数根分别为x1=-2,x2=4,则m+n的值是( )
| A. | -10 | B. | 10 | C. | -6 | D. | 2 |
12.当0<x<1时,x,$\frac{1}{x}$,x2的大小顺序是( )
| A. | $\frac{1}{x}$<x<x2 | B. | x<x2<$\frac{1}{x}$ | C. | x2<x<$\frac{1}{x}$ | D. | $\frac{1}{x}$<x2<x |
16.下列图形是将正三角形按一定规律排列,则第4个图形中所有正三角形的个数有( )
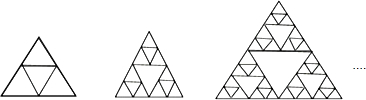

| A. | 160 | B. | 161 | C. | 162 | D. | 163 |
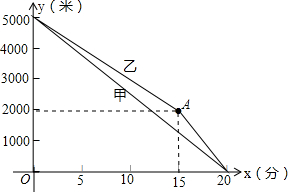 甲、乙两名运动员进行长跑训练,两人距终点的路程y(米)与跑步时间x(分)之间的函数关系如图所示,根据图象所提供的信息解答问题:
甲、乙两名运动员进行长跑训练,两人距终点的路程y(米)与跑步时间x(分)之间的函数关系如图所示,根据图象所提供的信息解答问题:
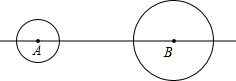 如图,在直线上有A、B两点,AB=10cm,⊙A的半径是1cm,⊙B的半径是2cm,⊙A以3cm/s的速度向右运动,同时⊙B以1cm/s的速度向右运动.设运动时间为t秒,当⊙A与⊙B相切时,t的值是3.5、4.5、5.5、6.5.
如图,在直线上有A、B两点,AB=10cm,⊙A的半径是1cm,⊙B的半径是2cm,⊙A以3cm/s的速度向右运动,同时⊙B以1cm/s的速度向右运动.设运动时间为t秒,当⊙A与⊙B相切时,t的值是3.5、4.5、5.5、6.5.