题目内容
10.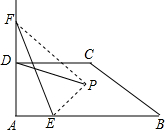 如图,四边形纸片ABCD中,AB∥CD,AD⊥AB,AB=10,AD=2$\sqrt{3}$,CD=4,点E是线段AB上的一动点,点F是射线AD上的一动点.将△AEF沿EF翻折,点A的落点记为P,连接PD.
如图,四边形纸片ABCD中,AB∥CD,AD⊥AB,AB=10,AD=2$\sqrt{3}$,CD=4,点E是线段AB上的一动点,点F是射线AD上的一动点.将△AEF沿EF翻折,点A的落点记为P,连接PD.(1)当AE=4,且点P刚好落在CD边上时,则线段PD长为2;
(2)若点P始终落在四边形ABCD内部,则线段PD长的变化范围是$\frac{4\sqrt{13}-10}{3}<PD<\frac{2\sqrt{127}}{3}$.
分析 (1)首先根据题意画出图形,由题意可证明四边形AECD为矩形,然后在Rt△PCE中,由勾股定理得PC=2,从而可求得DP的长;
(2)点P和点A关于EF对称,所以PE=AE,从而可知点P在以E为圆心,以AE为半径的圆上,然后再求得点E到DC和BC的距离,从而可确定出AE的长,然后计算出DP1、DP2的长度从而可确定出DP的范围.
解答 解:(1)如图1,连接EC.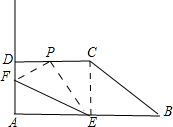
图1
∵AB∥DC,DC=AE=4,
∴四边形AECD为平行四边形.
又∵AD⊥AB,
∴四边形AECD为矩形.
∴CE⊥DC、CE=AD=2$\sqrt{3}$.
由折叠的性质可知:PE=AE=4,
在Rt△PCE中,由勾股定理得PC=$\sqrt{P{E}^{2}-C{E}^{2}}$=$\sqrt{{4}^{2}-(2\sqrt{3})^{2}}$=2,
∴PD=DC-PC=4-2=2.
(2)∵点P和点A关于EF对称,
∴PE=AE.
∴点P在以E为圆心,以AE为半径的圆上.
如图2: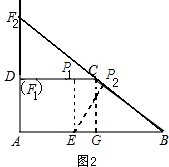
当点F运动到F1时,点F1与点D重合时,点P1在线段DC上,由(1)可知AEP1D为矩形,
∴EP1=2$\sqrt{3}$,
过点C作CG⊥AB,由(1)可知四边形DAGC为矩形,
∴CG=2$\sqrt{3}$.
在Rt△BCG中,BC=$\sqrt{C{G}^{2}+B{G}^{2}}=\sqrt{{6}^{2}+(2\sqrt{3})^{2}}$=4$\sqrt{3}$.
当点F运动到F2时,点B、C、F2在一条上,由折叠的性质可知:∠F2P2E=∠A=90°,设AE=x,则EP2=x,EB=10-x,
∴∠F2P2E=∠CGB=90°,
又∵∠B=∠B,
∴△EBP2∽△CBG.
∴$\frac{BC}{BE}=\frac{CG}{E{P}_{2}}$即:$\frac{4\sqrt{3}}{10-x}=\frac{2\sqrt{3}}{x}$.
∴x=$\frac{10}{3}$.
∵$\frac{10}{3}<2\sqrt{3}$,
∴当AE<$\frac{10}{3}$时,点P一定在四边形ABCD内.
∴点P在以E为圆心,以$\frac{10}{3}$为半径的圆内.
如图3: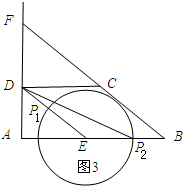
在Rt△ADE中,DE=$\sqrt{A{D}^{2}+A{E}^{2}}=\sqrt{(2\sqrt{3})^{2}+(\frac{10}{3})}$=$\frac{4\sqrt{13}}{3}$,
在Rt△ADE中,DP2=$\sqrt{A{D}^{2}+A{{P}_{2}}^{2}}$=$\sqrt{(2\sqrt{3})^{2}+(\frac{20}{3})^{2}}$=$\frac{2\sqrt{127}}{3}$,
当点P位于点P1处时,PD有最小值,PD=DP1=DE-EP1=$\frac{4\sqrt{13}-10}{3}$,
当点P位于点P2处时,PD有最大值,PD=DP2=$\frac{2\sqrt{127}}{3}$.
∴点DP的位置范围为:$\frac{4\sqrt{13}-10}{3}<DP<\frac{2\sqrt{127}}{3}$.
故答案为:(1)2;(2)$\frac{4\sqrt{13}-10}{3}<DP<\frac{2\sqrt{127}}{3}$.
点评 本题主要考查了轴对称的性质,相似三角形的性质和判定、勾股定理以及圆的定义,求得点E到DC和BC的距离,从而可确定出AE的长度是解题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | -10 | B. | 10 | C. | -6 | D. | 2 |
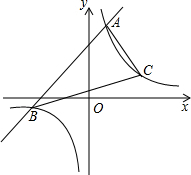 已知一次函数y1=x+m的图象与反比例函数y2=$\frac{6}{x}$的图象交于A、B两点,已知当x>1时,y1>y2;当0<x<1时,y1<y2.
已知一次函数y1=x+m的图象与反比例函数y2=$\frac{6}{x}$的图象交于A、B两点,已知当x>1时,y1>y2;当0<x<1时,y1<y2.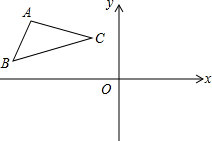 如图,已知△ABC和过点O的两条互相垂直的直线x、y,画出△ABC关于直线x对称的△A′B′C′,再画出△A′B′C′关于点O成中心对称的△A″B″C″.
如图,已知△ABC和过点O的两条互相垂直的直线x、y,画出△ABC关于直线x对称的△A′B′C′,再画出△A′B′C′关于点O成中心对称的△A″B″C″.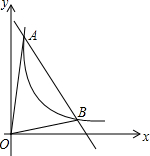 如图,一次函数y=kx+b与反比例函数y=$\frac{6}{x}$(x>0)的图象交于A(m,6),B(3,n)两点.
如图,一次函数y=kx+b与反比例函数y=$\frac{6}{x}$(x>0)的图象交于A(m,6),B(3,n)两点.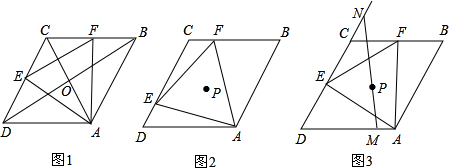
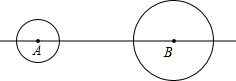 如图,在直线上有A、B两点,AB=10cm,⊙A的半径是1cm,⊙B的半径是2cm,⊙A以3cm/s的速度向右运动,同时⊙B以1cm/s的速度向右运动.设运动时间为t秒,当⊙A与⊙B相切时,t的值是3.5、4.5、5.5、6.5.
如图,在直线上有A、B两点,AB=10cm,⊙A的半径是1cm,⊙B的半径是2cm,⊙A以3cm/s的速度向右运动,同时⊙B以1cm/s的速度向右运动.设运动时间为t秒,当⊙A与⊙B相切时,t的值是3.5、4.5、5.5、6.5.