题目内容
20.(1)解方程:$\frac{x}{x-1}$=$\frac{3}{(x-1)(x+2)}$+1(2)化简求值:$\frac{x+3}{{x}^{2}-1}$•$\frac{{x}^{2}+2x+1}{x+3}$-($\frac{1}{x-1}$+1),其中x=-2.
分析 (1)先把方程两边乘以(x-1)(x+2)得到x(x+2)=3+(x-1)(x+2),然后解此一次方程后进行检验确定原方程的解;
(2)先把括号内通分和把分子分母因式分解,再约分得到原式=$\frac{1}{x-1}$,然后把x的值代入计算即可.
解答 解:(1)去分母得x(x+2)=3+(x-1)(x+2),
解得x=1,
检验:当x=1时,(x-1)(x+2)=0,所以x=1是原方程的增根,
所以原方程无解;
(2)因式=$\frac{x+3}{(x+1)(x-1)}$•$\frac{(x+1)^{2}}{x+3}$-$\frac{1+x-1}{x-1}$
=$\frac{x+1}{x-1}$-$\frac{x}{x-1}$
=$\frac{1}{x-1}$,
当x=-2时,原式=$\frac{1}{-2-1}$=-$\frac{1}{3}$.
点评 本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.也考查了解分式方程.

练习册系列答案
相关题目
8.把弯曲的道路改直,就能缩短两点之间的距离,其中蕴含的数学原理是( )
| A. | 两点确定一条直线 | B. | 两点之间线段最短 | ||
| C. | 过一点有无数条直线 | D. | 线段是直线的一部分 |
15.若分式$\frac{x-1}{x-3}$有意义,则x满足的条件是( )
| A. | x=1 | B. | x=3 | C. | x≠1 | D. | x≠3 |
12.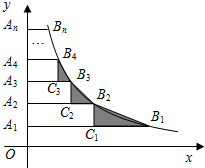 如图,在y轴正半轴上依次截取OA1=A1A2=A2A3=…=An-1An(n为正整数),过A1,A2,A3,…,An分别作x轴的平行线,与反比例函数y=$\frac{2}{x}$(x>0)交于点B1,B2,B3,…,Bn,如图所示的Rt△B1C1B2,Rt△B2C2B3,Rt△B3C3B4,…,Rt△Bn-1Cn-1Bn面积分别记为S1,S2,S3,…,Sn-1,则S1+S2+S3+…+Sn-1=( )
如图,在y轴正半轴上依次截取OA1=A1A2=A2A3=…=An-1An(n为正整数),过A1,A2,A3,…,An分别作x轴的平行线,与反比例函数y=$\frac{2}{x}$(x>0)交于点B1,B2,B3,…,Bn,如图所示的Rt△B1C1B2,Rt△B2C2B3,Rt△B3C3B4,…,Rt△Bn-1Cn-1Bn面积分别记为S1,S2,S3,…,Sn-1,则S1+S2+S3+…+Sn-1=( )
 如图,在y轴正半轴上依次截取OA1=A1A2=A2A3=…=An-1An(n为正整数),过A1,A2,A3,…,An分别作x轴的平行线,与反比例函数y=$\frac{2}{x}$(x>0)交于点B1,B2,B3,…,Bn,如图所示的Rt△B1C1B2,Rt△B2C2B3,Rt△B3C3B4,…,Rt△Bn-1Cn-1Bn面积分别记为S1,S2,S3,…,Sn-1,则S1+S2+S3+…+Sn-1=( )
如图,在y轴正半轴上依次截取OA1=A1A2=A2A3=…=An-1An(n为正整数),过A1,A2,A3,…,An分别作x轴的平行线,与反比例函数y=$\frac{2}{x}$(x>0)交于点B1,B2,B3,…,Bn,如图所示的Rt△B1C1B2,Rt△B2C2B3,Rt△B3C3B4,…,Rt△Bn-1Cn-1Bn面积分别记为S1,S2,S3,…,Sn-1,则S1+S2+S3+…+Sn-1=( )| A. | 1 | B. | 2 | C. | 1-$\frac{1}{n}$ | D. | 2-$\frac{1}{n}$ |
10.如图由圆形组成的四个图形中,可以看做是中心对称图形的有( )


| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
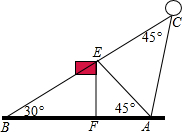 如图,某校20周年校庆时,需要在草场上利用气球悬挂宣传条幅,EF为旗杆,气球从A处起飞,几分钟后便飞达C处,此时,在AF延长线上的点B处测得气球和旗杆EF的顶点E在同一直线上.
如图,某校20周年校庆时,需要在草场上利用气球悬挂宣传条幅,EF为旗杆,气球从A处起飞,几分钟后便飞达C处,此时,在AF延长线上的点B处测得气球和旗杆EF的顶点E在同一直线上. 已知点A坐标为(-2,4),点B坐标为(-2,0)点C坐标为(0,1)
已知点A坐标为(-2,4),点B坐标为(-2,0)点C坐标为(0,1)