题目内容
11.化简下列式子,使结果只含有正整数指数幂:(4a-2b3)2(-2a2b-3)=-$\frac{32{b}^{3}}{{a}^{2}}$(a≠0,b≠0).分析 首先利用积的乘方计算(4a-2b3)2,再根据单项式乘以单项式计算16a-4b6•(-2a2b-3),最后再把负指数变为正指数即可.
解答 解:原式=16a-4b6•(-2a2b-3)=-32a-2b3=-$\frac{32{b}^{3}}{{a}^{2}}$,
故答案为:-$\frac{32{b}^{3}}{{a}^{2}}$.
点评 此题主要考查了负整数指数幂,关键是掌握a-p=$\frac{1}{{a}^{p}}$(a≠0,p为正整数).

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
2.观察下列图形:

它们是按一定规律排列的,依照此规律,第n个图形中共有( )个五角星(n为正整数).

它们是按一定规律排列的,依照此规律,第n个图形中共有( )个五角星(n为正整数).
| A. | 4+3(n-1) | B. | 4n | C. | 4n+1 | D. | 3n+4 |
6.下列计算不正确的是( )
| A. | 5a3-a3=4a3 | B. | a3•a3=a6 | C. | ($\frac{{a}^{2}{b}^{3}}{c}$)2=$\frac{{a}^{4}{b}^{6}}{c}$ | D. | a6÷a3=a3 |
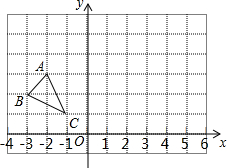 △ABC在平面直角坐标系中的位置如图所示.
△ABC在平面直角坐标系中的位置如图所示. Rt△ABC中,∠B=90°,AD平分∠BAC,DE⊥AC于E,若BC=8,DE=3,则CD的长度是5.
Rt△ABC中,∠B=90°,AD平分∠BAC,DE⊥AC于E,若BC=8,DE=3,则CD的长度是5. 如图所示:已知O为AB上一点,∠BOC=46°,OD平分∠AOC,∠AOD=67°.
如图所示:已知O为AB上一点,∠BOC=46°,OD平分∠AOC,∠AOD=67°.