Question

5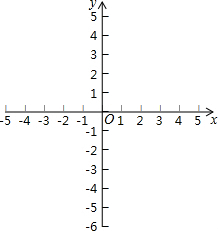．已知点A坐标为（-2，4），点B坐标为（-2，0）点C坐标为（0，1）
（1）在平面直角坐标系xOy中描出点A、点B及点C的坐标．
（2）作出A、B两点关于y轴对称的对称点A₁、B₁的坐标，作出C点关于x轴对称的对称点C₁的坐标．
（3）连接A₁B₁、B₁C₁、A₁C₁，直接写出△A₁B₁C₁的面积．

Answer 1

分析 （1）根据坐标点结合坐标系确定点A、点B及点C的位置；
（2）根据关于x轴对称：横坐标不变，纵坐标相反；关于y轴对称：纵坐标不变，横坐标相反可得点A₁、B₁的坐标，点C₁的坐标，然后再描出点的位置即可；
（3）首先画出图形，再利用矩形的面积减去周围多余三角形的面积即可．

解答 解：（1）如图所示：

（2）A₁（2，4），B₁（2，0），C₁（0，-1）．

（3）△A₁B₁C₁的面积为：5×2-$\frac{1}{2}×$2×5-$\frac{1}{2}$×1×2=4．

点评 此题主要考查了作图--轴对称变换，关键是掌握关于坐标轴对称的点的坐标规律．