题目内容
9.如果a是不为1的数,我们把$\frac{1}{1-a}$称为a的差倒数,如:2的差倒数为$\frac{1}{1-2}=-1$;-1的差倒数是$\frac{1}{{1-({-1})}}=\frac{1}{2}$;已知a1=4,a2是a1的差倒数,a3是a2的差倒数,a4是a3差倒数,…,依此类推,则a5=$-\frac{1}{3}$,a2016=$\frac{3}{4}$.分析 首先根据新定义规则求出a1,a2,a3,a4,a5找到存在的循环性规律,求解即可.
解答 解:a1=4,a2=$\frac{1}{1-4}$=$-\frac{1}{3}$,a3=$\frac{1}{1-(-\frac{1}{3})}$=$\frac{3}{4}$,a4=$\frac{1}{1-\frac{3}{4}}$=4,a5=$\frac{1}{1-4}$=$-\frac{1}{3}$;
可知:数列以“4,$-\frac{1}{3}$,$\frac{3}{4}$”三个数循环出现,
2016÷3=672(整除),所以a2016=$\frac{3}{4}$.
故答案为:$-\frac{1}{3}$,$\frac{3}{4}$.
点评 此题主要考查新定义运算和数列的规律探索,准确应用新定义进行计算并找出存在的循环性规律是解题的关键.

练习册系列答案
相关题目
4.已知代数式-5am-1b6与$\frac{1}{2}a{b^n}$是同类项,那么m-n的值是( )
| A. | 5 | B. | -5 | C. | 4 | D. | -4 |
18. 如图,图中数字表示所在正方形的面积,则字母B所代表的正方形的面积是( )
如图,图中数字表示所在正方形的面积,则字母B所代表的正方形的面积是( )
 如图,图中数字表示所在正方形的面积,则字母B所代表的正方形的面积是( )
如图,图中数字表示所在正方形的面积,则字母B所代表的正方形的面积是( )| A. | 196 | B. | 144 | C. | 13 | D. | 12 |
19.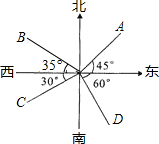 如图,下列说法中错误的是( )
如图,下列说法中错误的是( )
 如图,下列说法中错误的是( )
如图,下列说法中错误的是( )| A. | OA的方向是东北方向 | B. | OB的方向是北偏西55° | ||
| C. | OC的方向是南偏西30° | D. | OD的方向是南偏东30° |
 如图所示:已知O为AB上一点,∠BOC=46°,OD平分∠AOC,∠AOD=67°.
如图所示:已知O为AB上一点,∠BOC=46°,OD平分∠AOC,∠AOD=67°.