Question

12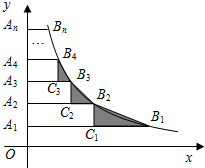．如图，在y轴正半轴上依次截取OA₁=A₁A₂=A₂A₃=…=A_n-1A_n（n为正整数），过A₁，A₂，A₃，…，A_n分别作x轴的平行线，与反比例函数y=$\frac{2}{x}$（x＞0）交于点B₁，B₂，B₃，…，B_n，如图所示的Rt△B₁C₁B₂，Rt△B₂C₂B₃，Rt△B₃C₃B₄，…，Rt△B_n-1C_n-1B_n面积分别记为S₁，S₂，S₃，…，S_n-1，则S₁+S₂+S₃+…+S_n-1=（　　）

• A． 1
• B． 2
• C． 1-$\frac{1}{n}$
• D． 2-$\frac{1}{n}$

Answer 1

分析 设OA₁=A₁A₂=A₂A₃=…=A_n-1A_n=a，确定A₁，A₂，A₃，A₄的横坐标，根据反比例函数的解析式求出A₁，A₂，A₃，A₄的坐标，根据反比例函数系数k的几何意义求出三角形的面积之和．

解答 解：设OA₁=A₁A₂=A₂A₃=…=A_n-1A_n=a，
由题意得，
B₁（$\frac{2}{a}$，a），B₂（$\frac{2}{2a}$，2a），B₃（$\frac{2}{3a}$，3a），B₄（$\frac{2}{4a}$，4a），…，B_n（$\frac{2}{na}$，na），
则S₁+S₂+S₃+…+S_n-1=$\frac{1}{2}$×（$\frac{2}{a}$-$\frac{2}{2a}$）×a+$\frac{1}{2}$×（$\frac{2}{2a}$-$\frac{2}{3a}$）×a+$\frac{1}{2}$×（$\frac{2}{3a}$-$\frac{2}{4a}$）×a+…+$\frac{1}{2}$×（$\frac{2}{（n-1）a}$-$\frac{2}{na}$）×a
=1-$\frac{1}{n}$，
故选C．

点评 本题考查的是反比例函数系数k的几何意义，反比例函数y=$\frac{k}{x}$中k的几何意义，即过双曲线上任意一点引x轴、y轴垂线，所得三角形面积为$\frac{1}{2}$|k|，是经常考查的一个知识点；这里体现了数形结合的思想，做此类题一定要正确理解k的几何意义．