题目内容
10.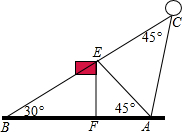 如图,某校20周年校庆时,需要在草场上利用气球悬挂宣传条幅,EF为旗杆,气球从A处起飞,几分钟后便飞达C处,此时,在AF延长线上的点B处测得气球和旗杆EF的顶点E在同一直线上.
如图,某校20周年校庆时,需要在草场上利用气球悬挂宣传条幅,EF为旗杆,气球从A处起飞,几分钟后便飞达C处,此时,在AF延长线上的点B处测得气球和旗杆EF的顶点E在同一直线上.(1)已知旗杆高为12米,若在点B处测得旗杆顶点E的仰角为30°,A处测得点E的仰角为45°,试求AB的长(结果保留根号);
(2)在(1)的条件下,若∠BCA=45°,绳子在空中视为一条线段,试求绳子AC的长(结果保留根号)?
分析 (1)在直角△BEF中首先求得BF,然后在直角△AEF中求得AF,根据AB=BF+AF即可求解;
(2)作AG⊥BC于点G,在直角△ABG中首先求得AG,然后在直角△AGC中利用三角函数求解.
解答  解:(1)∵在直角△BEF中,tan∠EBF=$\frac{EF}{BF}$,
解:(1)∵在直角△BEF中,tan∠EBF=$\frac{EF}{BF}$,
∴BE=$\frac{EF}{tan∠EBA}$$\frac{EF}{tan30°}$=$\frac{EF}{sin30°}$=12$\sqrt{3}$.
同理AF=EF=12(米),
则AB=BF+AF=12$\sqrt{3}$+12(米);
(2)作AG⊥BE于点G,
在直角△ABG中,AG=AB•sin30°=$\frac{1}{2}$(12$\sqrt{3}$+12)=6$\sqrt{3}$+6.
又∵直角△AGC中,∠ACG=45°,
∴AC=$\sqrt{2}$AG=6$\sqrt{6}$+6$\sqrt{2}$(米).
点评 本题考查了仰角、俯角的概念,要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
相关题目
18.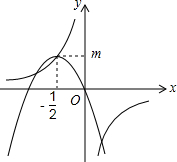 如图,双曲线y=$\frac{k}{x}$经过抛物线y=ax2+bx的顶点(-$\frac{1}{2}$,m)(m>0),则有( )
如图,双曲线y=$\frac{k}{x}$经过抛物线y=ax2+bx的顶点(-$\frac{1}{2}$,m)(m>0),则有( )
 如图,双曲线y=$\frac{k}{x}$经过抛物线y=ax2+bx的顶点(-$\frac{1}{2}$,m)(m>0),则有( )
如图,双曲线y=$\frac{k}{x}$经过抛物线y=ax2+bx的顶点(-$\frac{1}{2}$,m)(m>0),则有( )| A. | a=b+2k | B. | a=b-2k | C. | k<b<0 | D. | a<k<0 |
5. 如图,每个小正方形的边长均为1,△ABC和△DEC的顶点均在“格点”上,则$\frac{△DEC周长}{△ABC周长}$=( )
如图,每个小正方形的边长均为1,△ABC和△DEC的顶点均在“格点”上,则$\frac{△DEC周长}{△ABC周长}$=( )
 如图,每个小正方形的边长均为1,△ABC和△DEC的顶点均在“格点”上,则$\frac{△DEC周长}{△ABC周长}$=( )
如图,每个小正方形的边长均为1,△ABC和△DEC的顶点均在“格点”上,则$\frac{△DEC周长}{△ABC周长}$=( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |
2.观察下列图形:

它们是按一定规律排列的,依照此规律,第n个图形中共有( )个五角星(n为正整数).

它们是按一定规律排列的,依照此规律,第n个图形中共有( )个五角星(n为正整数).
| A. | 4+3(n-1) | B. | 4n | C. | 4n+1 | D. | 3n+4 |
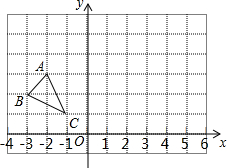 △ABC在平面直角坐标系中的位置如图所示.
△ABC在平面直角坐标系中的位置如图所示.