题目内容
7. 如图,已知点A是一次函数y=x的图象与反比例函数y=$\frac{2}{x}$的图象在第一象限内的交点,点B在x轴的负半轴上且OA=OB.
如图,已知点A是一次函数y=x的图象与反比例函数y=$\frac{2}{x}$的图象在第一象限内的交点,点B在x轴的负半轴上且OA=OB.(1)求A点的坐标;
(2)求△AOB的面积;
(3)直接写出一次函数y=x大于反比例函数y=$\frac{2}{x}$时x的取值范围.
分析 (1)联立一次函数与反比例函数的解析式,求出x的值即可得出A点坐标;
(2)求出OA的长,根据OA=OB即可得出OB的长,利用三角形的面积公式即可得出结论;
(3)根据反比例函数的对称性得出直线与抛物线另一个交点的坐标,利用函数图象可直接得出结论.
解答 解:(1)∵点A是一次函数y=x的图象与反比例函数y=$\frac{2}{x}$的图象在第一象限内的交点,
∴$\left\{\begin{array}{l}y=x\\ y=\frac{2}{x}\end{array}\right.$,解得x=±$\sqrt{2}$,
∵点A在第一象限,
∴x=$\sqrt{2}$,
∴A($\sqrt{2}$,$\sqrt{2}$);
(2)∵OA=$\sqrt{(\sqrt{2})^{2}+(\sqrt{2})^{2}}$=$\sqrt{2+2}$=2,OA=OB,
∴OA=OB=2,
∴S△AOB=$\frac{1}{2}$×2×$\sqrt{2}$=$\sqrt{2}$;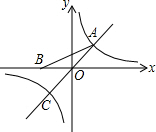
(3)∵反比例函数与正比例函数的图象均关于原点对称,A($\sqrt{2}$,$\sqrt{2}$),
∴C(-$\sqrt{2}$,-$\sqrt{2}$).
由函数图象可知,当x>$\sqrt{2}$或-$\sqrt{2}$<x<0时,一次函数y=x大于反比例函数y=$\frac{2}{x}$.
点评 本题考查的是正比例函数与反比例函数图象的交点问题,熟知反比例函数与正比例函数的图象均关于原点对称是解答此题的关键.

练习册系列答案
相关题目
17.若关于x的方程x2+2x+a=0有两个实数根,则a的取值范围是( )
| A. | a<1 | B. | a>1 | C. | a≤1 | D. | a≥1 |
18.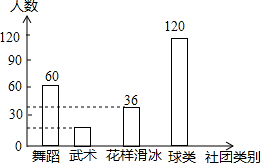 某校开展社团活动,准备组件舞蹈、武术、球类(足球、篮球、乒乓球、羽毛球).花样滑冰四类社团,为了解在校学生对这4个社团活动的喜爱情况,学校随机抽取部分学生进行了“你最喜爱的社团”调查,依据相关数据绘制以下的统计图表,请根据图表中的信息解答下列问题:
某校开展社团活动,准备组件舞蹈、武术、球类(足球、篮球、乒乓球、羽毛球).花样滑冰四类社团,为了解在校学生对这4个社团活动的喜爱情况,学校随机抽取部分学生进行了“你最喜爱的社团”调查,依据相关数据绘制以下的统计图表,请根据图表中的信息解答下列问题:
“你最喜爱的社团”调查统计图表
(1)被调查的学生总人数是240;m=24,n=15.
(2)被调查喜爱球类的学生中有12人最喜爱乒乓球,若该校有2600名学生,试估计全校最喜爱乒乓球的人数.
 某校开展社团活动,准备组件舞蹈、武术、球类(足球、篮球、乒乓球、羽毛球).花样滑冰四类社团,为了解在校学生对这4个社团活动的喜爱情况,学校随机抽取部分学生进行了“你最喜爱的社团”调查,依据相关数据绘制以下的统计图表,请根据图表中的信息解答下列问题:
某校开展社团活动,准备组件舞蹈、武术、球类(足球、篮球、乒乓球、羽毛球).花样滑冰四类社团,为了解在校学生对这4个社团活动的喜爱情况,学校随机抽取部分学生进行了“你最喜爱的社团”调查,依据相关数据绘制以下的统计图表,请根据图表中的信息解答下列问题:“你最喜爱的社团”调查统计图表
| 社团类别 | 人数 | 占总人数的比例 |
| 舞蹈 | 60 | 25% |
| 武术 | m | 10% |
| 花样滑冰 | 36 | n% |
| 球类 | 120 | 50% |
(2)被调查喜爱球类的学生中有12人最喜爱乒乓球,若该校有2600名学生,试估计全校最喜爱乒乓球的人数.
2. 某射击小组有19人,教练根据他们某次射击的数据绘制成如图所示的统计图,则这组数据的众数和中位数分别是( )
某射击小组有19人,教练根据他们某次射击的数据绘制成如图所示的统计图,则这组数据的众数和中位数分别是( )
 某射击小组有19人,教练根据他们某次射击的数据绘制成如图所示的统计图,则这组数据的众数和中位数分别是( )
某射击小组有19人,教练根据他们某次射击的数据绘制成如图所示的统计图,则这组数据的众数和中位数分别是( )| A. | 7,7 | B. | 8,7.5 | C. | 7,8 | D. | 8,7 |
17.射线AD、AE分别与⊙O相切于D、E两点,直线BC与⊙O相切于点F,分别交AD、AE于点B、C,若∠A=40°.则∠BOC等于( )
| A. | 70° | B. | 110° | C. | 70°或110° | D. | 40°或140° |
