题目内容
8.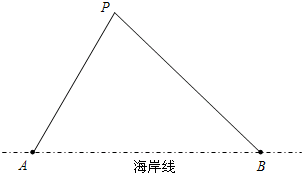 捍卫祖国海疆是人民海军的神圣职责.我海军在相距20海里的A、B两地设立观测站(海岸线是过A、B的直线).按国际惯例,海岸线以外12海里范围内均为我国领海,外国船只除特许外,不得私自进入我国领海.某日,观测员发现一外国船只行驶至P处,在A观测站测得∠BAP=63°,同时在B观测站测得∠ABP=34°.问此时是否需要向此未经特许的船只发出警告,命令其退出我国领海?(参考数据:sin63°≈$\frac{9}{10}$,tan63°≈2,sin34°≈$\frac{3}{5}$,tan34°≈$\frac{2}{3}$)
捍卫祖国海疆是人民海军的神圣职责.我海军在相距20海里的A、B两地设立观测站(海岸线是过A、B的直线).按国际惯例,海岸线以外12海里范围内均为我国领海,外国船只除特许外,不得私自进入我国领海.某日,观测员发现一外国船只行驶至P处,在A观测站测得∠BAP=63°,同时在B观测站测得∠ABP=34°.问此时是否需要向此未经特许的船只发出警告,命令其退出我国领海?(参考数据:sin63°≈$\frac{9}{10}$,tan63°≈2,sin34°≈$\frac{3}{5}$,tan34°≈$\frac{2}{3}$)
分析 过P作PH垂直于AB,交AB于H点,设PH=x海里,在直角三角形APH中,由∠BAP=63°,利用正切函数定义表示出AH,再由∠ABP=34°,得出HB,再根据AH+HB=AB,求出x的值,再与12海里进行比较,即可得出答案.
解答 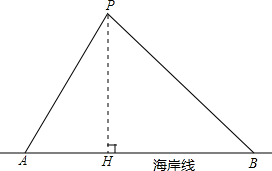 解:过P作PH⊥AB于H,如图所示,
解:过P作PH⊥AB于H,如图所示,
设AH=x海里,
在Rt△APH中,∠BAP=63°,
∴PH=AH•tan63°=2x(海里),
∵∠ABP=34°,∠PHB=90°,
∴tan34°=$\frac{PH}{HB}$,
∴HB=3x(海里),
又∵AB=20海里,
∴2x+3x=20,
解得:x=4,
∴PH=4(海里)<12(海里),
则此时需要向该船发出警告.
点评 此题考查了解直角三角形的应用-方向角问题,用到的知识点是锐角三角形函数定义,等腰直角三角形的判定与性质,其中作出相应的辅助线是本题的关键.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
16. 如图,等边三角形ABC中,点D,E分别为AB,AC的中点,则∠DEC的度数为( )
如图,等边三角形ABC中,点D,E分别为AB,AC的中点,则∠DEC的度数为( )
 如图,等边三角形ABC中,点D,E分别为AB,AC的中点,则∠DEC的度数为( )
如图,等边三角形ABC中,点D,E分别为AB,AC的中点,则∠DEC的度数为( )| A. | 150° | B. | 120° | C. | 60° | D. | 30° |
3.若代数式x+5的值是2,则x等于( )
| A. | 3 | B. | -3 | C. | -5 | D. | -7 |
13.在平面直角坐标系中,点P(-3,a2+1)所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
17.在平面直角坐标系中,点P的横坐标是-3,且点P到x轴的距离为5,则点P的坐标是( )
| A. | (5,-3)或(-5,-3) | B. | (-3,5)或(-3,-5) | C. | (-3,5) | D. | (-3,-5) |
18. 如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处,若∠B=68°,则∠BDC=( )
如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处,若∠B=68°,则∠BDC=( )
 如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处,若∠B=68°,则∠BDC=( )
如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处,若∠B=68°,则∠BDC=( )| A. | 44° | B. | 60° | C. | 67° | D. | 77° |
 某中学综合实践小组同学,想测量金龙山观音大佛的高度,他们在山脚下的D处测得山顶B的仰角为30°,沿着山脚向前走了4米达到E处,测得观音大佛的头顶A的倾角为45°,已知金龙山的山顶距地面的标高(线段BC的长度)为60米,请计算观音大佛的高度为多少米?(结果精确到0.1米,$\sqrt{3}$≈1.73)
某中学综合实践小组同学,想测量金龙山观音大佛的高度,他们在山脚下的D处测得山顶B的仰角为30°,沿着山脚向前走了4米达到E处,测得观音大佛的头顶A的倾角为45°,已知金龙山的山顶距地面的标高(线段BC的长度)为60米,请计算观音大佛的高度为多少米?(结果精确到0.1米,$\sqrt{3}$≈1.73)