��Ŀ����
14����ͼ���ھ���OABC�У���A��C�ֱ���x���ϣ�y���ϣ���B����Ϊ��4��2����DΪBC��һ���㣬�ѡ�OCD��OD���ۣ���C���ڵ�P�����γ���ͼ�������Σ�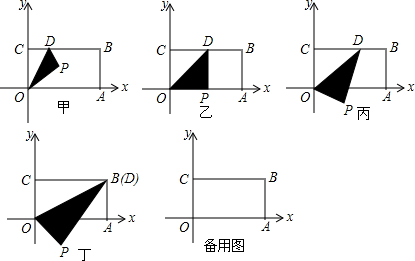
��1����ͼ��������D�˶������B�غ�ʱ�����P�����ꣻ
��2������ֱ��y=kx+2$\sqrt{2}$���۲��D�ӵ�C���B�˶������У���P���γɵ��˶�·��ͼ�Σ���ֱ��y=kx+2$\sqrt{2}$���P���γɵ��˶�·��ͼ����2��������ʱ����k��ȡֵ��Χ��
���� ��1��������BP��x��Ľ���Ϊ��E���ٸ���ȫ�������ε��ж��������жϳ���OPE�ա�BAE��Ȼ����OE=x����BE=x��AE=4-x�����OE��PE��ֵ���Ƕ��٣�������RT��OPE�У�OE-PF=OP-PE�����PF��ֵ�Ƕ��٣��ٸ��ݡ�OPF�ס�OEP����$\frac{PF}{OF}=\frac{PE}{OP}$�����OF��ֵ�Ƕ��٣����������P�����꼴�ɣ�
��2����D�ӵ�C���B�˶������У���P���γɵ��˶�·��ͼ������OΪԲ�ģ�2Ϊ�뾶�Ļ�������P2�����꼴�ڣ�1�����е�P�����꣬��${P}_{2}��\frac{8}{5}��-\frac{6}{5}��$����P1��ֱ��y=kx+2$\sqrt{2}$�뻡���е��е㣬����OP1����P1��P1H��x�ᣬOK=2$\sqrt{2}$��OP1=2�����P1�����꣬�ٰ�P1��P2������ֱ����y=kx+2$\sqrt{2}$�����k1��k2��ֵ���жϳ�k��ȡֵ��Χ���ɣ�
��� �⣺��1����ͼ1����BP��x��Ľ���Ϊ��E��
��OP=BA����BAE=��OPE����BEA=��OEP��
���OPE�ա�BAE��
��OE=x����BE=x��AE=4-x��
����AE2+AB2=BE2��
�ɵã�4-x��2+22=x2��
���x=$\frac{5}{2}$��
��OE=$\frac{5}{2}$��PE2=OE2-OP2����PE=$\frac{3}{2}$��
RT��OPE�У�OE•PF=OP•PE��
��$\frac{5}{2}��PF=2��\frac{3}{2}$��
��PF=2��$\frac{3}{2}��\frac{5}{2}$
=3$��\frac{5}{2}$
=$\frac{6}{5}$��
���ݡ�OPF�ס�OEP����$\frac{PF}{OF}=\frac{PE}{OP}$��
��$\frac{\frac{6}{5}}{OF}=\frac{\frac{3}{2}}{2}$��
����OF=$\frac{6}{5}��2��\frac{3}{2}$
=$\frac{12}{5}��\frac{2}{3}$
=$\frac{8}{5}$��
��P��$\frac{8}{5}$��$-\frac{6}{5}$����
��2����ͼ2����D�ӵ�C���B�˶������У���P���γɵ��˶�·��ͼ������OΪԲ�ģ�2Ϊ�뾶�Ļ��� ��
��
����P2�����꼴�ڣ�1�����е�P�����꣬��${P}_{2}��\frac{8}{5}��-\frac{6}{5}��$��
��P1��ֱ��y=kx+2$\sqrt{2}$�뻡���е��е㣬����OP1����P1��P1H��x�ᣬOK=2$\sqrt{2}$��OP1=2��
���COP1=45�㣬��OP1H=45�㣬OH=P1H=$\sqrt{2}$��
��${P}_{1}��\sqrt{2}��\sqrt{2}��$��
��${P}_{1}��\sqrt{2}��\sqrt{2}��$��${P}_{2}��\frac{8}{5}��-\frac{6}{5}��$�ֱ����y=kx+2$\sqrt{2}$��
���k1=-1��${k}_{2}=-\frac{3}{4}-\frac{5\sqrt{2}}{4}$��
��-$\frac{3}{4}$-$\frac{5\sqrt{2}}{4}$��k��-1��
���� ��1��������Ҫ������һ�κ����ۺ��⣬�����˷������������������˴���֪����ͼ���л�ȡ��Ϣ���������û�ȡ����Ϣ�����Ӧ�������������
��2�����������ȫ�������ε��ж������ʣ��Լ�����˶��켣���жϣ�Ҫ�������գ�

| Xxx������ר�÷�Ʊ | |
| �Ʒ����ޣ�һ���� | |
| �õ������ȣ� | ��ۣ�Ԫ/�ȣ� |
| ����һ��190 | 0.53 |
| ���ݶ���190-290���������֣� | 0.58 |
| ����ʵ�ý�106.5��Ԫ�� | ����д��Ҽ����½Ԫ��� |
��1��������õ���x������ʾ��ʵ�������yԪ����ʾ������д��ʵ�������yԪ�����õ���x��֮��ĺ�����ϵʽ��
��2��������ݱ��б���ʵ�������������ͥ���µ�ʵ���õ�����
��3����Сǿ��С����һ���µ�ʵ���õ����ֱ�Ϊ120�Ⱥ�250�ȣ���ʵ�����ֱ�Ϊ����Ԫ��
 ��ͼ���ڡ�ABC�У�AD�ǽ�ƽ���ߣ�AE�Ǹߣ���BAC=40�㣬��C=60�㣬���DAE�Ķ�����
��ͼ���ڡ�ABC�У�AD�ǽ�ƽ���ߣ�AE�Ǹߣ���BAC=40�㣬��C=60�㣬���DAE�Ķ����� ��ͼ��������ABCD�����Ϊ4cm2����ͼ����Ӱ���ֵ����Ϊ2cm2��
��ͼ��������ABCD�����Ϊ4cm2����ͼ����Ӱ���ֵ����Ϊ2cm2�� ��ͼ����֪��ABC������AB=AC��
��ͼ����֪��ABC������AB=AC�� ��ͼ����ֱ��������ABC�У���C=90�㣬����DEFG���ĸ����㶼�ڡ�ABC�ı��ϣ���֪��AC=8��BC=6��
��ͼ����ֱ��������ABC�У���C=90�㣬����DEFG���ĸ����㶼�ڡ�ABC�ı��ϣ���֪��AC=8��BC=6��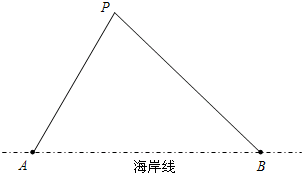 ���������������������ʥְ���Һ��������20�����A��B���������۲�վ���������ǹ�A��B��ֱ�ߣ��������ʹ���������������12���ﷶΧ�ھ�Ϊ�ҹ��캣�������ֻ�������⣬����˽�Խ����ҹ��캣��ij�գ��۲�Ա����һ�����ֻ��ʻ��P������A�۲�վ��á�BAP=63�㣬ͬʱ��B�۲�վ��á�ABP=34�㣮�ʴ�ʱ�Ƿ���Ҫ���δ�������Ĵ�ֻ�������棬�������˳��ҹ��캣�����ο����ݣ�sin63���$\frac{9}{10}$��tan63���2��sin34���$\frac{3}{5}$��tan34���$\frac{2}{3}$��
���������������������ʥְ���Һ��������20�����A��B���������۲�վ���������ǹ�A��B��ֱ�ߣ��������ʹ���������������12���ﷶΧ�ھ�Ϊ�ҹ��캣�������ֻ�������⣬����˽�Խ����ҹ��캣��ij�գ��۲�Ա����һ�����ֻ��ʻ��P������A�۲�վ��á�BAP=63�㣬ͬʱ��B�۲�վ��á�ABP=34�㣮�ʴ�ʱ�Ƿ���Ҫ���δ�������Ĵ�ֻ�������棬�������˳��ҹ��캣�����ο����ݣ�sin63���$\frac{9}{10}$��tan63���2��sin34���$\frac{3}{5}$��tan34���$\frac{2}{3}$��