题目内容
16. 如图,等边三角形ABC中,点D,E分别为AB,AC的中点,则∠DEC的度数为( )
如图,等边三角形ABC中,点D,E分别为AB,AC的中点,则∠DEC的度数为( )| A. | 150° | B. | 120° | C. | 60° | D. | 30° |
分析 根据等边三角形的性质,可得∠C的度数,根据三角形中位线的性质,可得DE与BC的关系,根据平行线的性质,可得答案.
解答 解:∵△ABC是等边三角形,
∴∠C=60°,
∵点D、E分别为边AB、AC的中点,
∴DE∥BC,
∴∠DEC=180°-∠C=180°-60°=120°,
故选:B.
点评 本题考查了三角形中位线定理以及等边三角形的性质,解题的关键是掌握三角形的中位线平行于第三边且等于第三边的一半.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.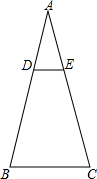 如图,在△ABC中,DE∥BC,且$\frac{AE}{EC}$=$\frac{1}{2}$,则$\frac{{S}_{四边形DBCE}}{{S}_{△ABC}}$=( )
如图,在△ABC中,DE∥BC,且$\frac{AE}{EC}$=$\frac{1}{2}$,则$\frac{{S}_{四边形DBCE}}{{S}_{△ABC}}$=( )
 如图,在△ABC中,DE∥BC,且$\frac{AE}{EC}$=$\frac{1}{2}$,则$\frac{{S}_{四边形DBCE}}{{S}_{△ABC}}$=( )
如图,在△ABC中,DE∥BC,且$\frac{AE}{EC}$=$\frac{1}{2}$,则$\frac{{S}_{四边形DBCE}}{{S}_{△ABC}}$=( )| A. | 1:4 | B. | 1:9 | C. | 3:4 | D. | 8:9 |
5.若$\sqrt{{a}^{2}}$=-a成立,则满足的条件是( )
| A. | a>0 | B. | a<0 | C. | a≥0 | D. | a≤0 |
6.下列运算正确的是( )
| A. | a3•a2=a5 | B. | (-a2)3=a6 | C. | (ab)3=ab3 | D. | a8÷a2=a4 |
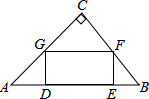 如图,在直角三角形ABC中,∠C=90°,矩形DEFG的四个顶点都在△ABC的边上,已知:AC=8,BC=6.
如图,在直角三角形ABC中,∠C=90°,矩形DEFG的四个顶点都在△ABC的边上,已知:AC=8,BC=6.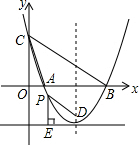 已知抛物线y=$\frac{1}{2}$x2+2(m+1)x-m+1与x轴交于点A、B,与y轴交于点C,其对称轴是直线x=4.
已知抛物线y=$\frac{1}{2}$x2+2(m+1)x-m+1与x轴交于点A、B,与y轴交于点C,其对称轴是直线x=4.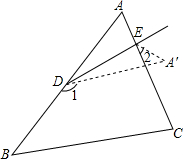 如图所示,将纸片△ABC沿DE折叠,点A落在点A′处,已知∠1=140°,∠2=40°,求∠A的度数.
如图所示,将纸片△ABC沿DE折叠,点A落在点A′处,已知∠1=140°,∠2=40°,求∠A的度数.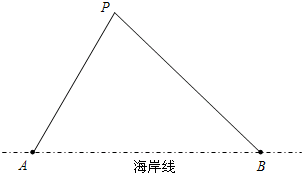 捍卫祖国海疆是人民海军的神圣职责.我海军在相距20海里的A、B两地设立观测站(海岸线是过A、B的直线).按国际惯例,海岸线以外12海里范围内均为我国领海,外国船只除特许外,不得私自进入我国领海.某日,观测员发现一外国船只行驶至P处,在A观测站测得∠BAP=63°,同时在B观测站测得∠ABP=34°.问此时是否需要向此未经特许的船只发出警告,命令其退出我国领海?(参考数据:sin63°≈$\frac{9}{10}$,tan63°≈2,sin34°≈$\frac{3}{5}$,tan34°≈$\frac{2}{3}$)
捍卫祖国海疆是人民海军的神圣职责.我海军在相距20海里的A、B两地设立观测站(海岸线是过A、B的直线).按国际惯例,海岸线以外12海里范围内均为我国领海,外国船只除特许外,不得私自进入我国领海.某日,观测员发现一外国船只行驶至P处,在A观测站测得∠BAP=63°,同时在B观测站测得∠ABP=34°.问此时是否需要向此未经特许的船只发出警告,命令其退出我国领海?(参考数据:sin63°≈$\frac{9}{10}$,tan63°≈2,sin34°≈$\frac{3}{5}$,tan34°≈$\frac{2}{3}$)