题目内容
17.某电脑公司经销甲种型号电脑,今年三月份的电脑售价比去年同期每台降价1000元,如果卖出相同数量的电脑,去年销售额为10万元,今年销售额只有8万元.(1)今年三月份甲种电脑每台售价多少元?
(2)为了增加收入,电脑公司决定再经销乙种型号电脑.已知甲种电脑每台进价为3500元,乙种电脑每台进价为3000元,公司预计用不多于5万元且不少于4.8万元的资金购进这两种电脑共15台,有几种进货方案?
分析 (1)根据单价=总价÷数量,列式计算即可得出结论;
(2)设购进甲种电脑y台,则购进乙种电脑(15-y)台(0≤y≤15),根据总价=甲种电脑单价×购买数量+乙种电脑单价×购买数量结合总价不多于5万元且不少于4.8万元即可得出关于y的一元一次不等式组,解之即可得出y的取值范围,取期内的正整数即可得出结论.
解答 解:(1)80000÷[(100000-80000)÷1000]=4000(元).
答:今年三月份甲种电脑每台售价4000元.
(2)设购进甲种电脑y台,则购进乙种电脑(15-y)台(0≤y≤15),
根据题意得:$\left\{\begin{array}{l}{3500y+3000(15-y)≥48000}\\{3500y+3000(15-y)≤50000}\end{array}\right.$,
解得:6≤y≤10,
∴y可以为6、7、8、9、10.
答:有五种进货方案.
点评 本题考查了分式方程的应用以及分式方程的应用,解题的关键是:(1)根据单价=总价÷数量列式计算;(2)根据总价的范围列出关于y的一元一次不等式组.

练习册系列答案
相关题目
6.已知二次函数y=(x-h)2+1(h为常数),在自变量x的值满足1≤x≤3的情况下,与其对应的函数y的最小值为5,则h的值是( )
| A. | -1 | B. | -1或5 | C. | 5 | D. | -5 |
12.直角三角形中,一直角边的长为6,斜边的长为9,那么斜边上的高将这个直角三角形分成的两个小三角形的面积比是( )
| A. | $\sqrt{5}$:2 | B. | 4:5 | C. | 3:5 | D. | 10:25 |
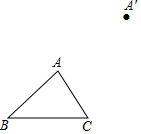 如图,平移三角形ABC,使点A移动到点A′,画出平移后的三角形A′B′C′.
如图,平移三角形ABC,使点A移动到点A′,画出平移后的三角形A′B′C′.
 已知反比例函数y=$\frac{kb}{x}$的图象如图所示,则一次函数y=kx+b的图象可能是( )
已知反比例函数y=$\frac{kb}{x}$的图象如图所示,则一次函数y=kx+b的图象可能是( )



 如图,E为正方形ABCD的边DC上一点,DE=2EC=2,将△BEC沿BE所在的直线对折得到△BEF,延长EF交BA的延长线于点M,则AM=2.
如图,E为正方形ABCD的边DC上一点,DE=2EC=2,将△BEC沿BE所在的直线对折得到△BEF,延长EF交BA的延长线于点M,则AM=2.