题目内容
12．在同一直角坐标平面内，直线y=x与双曲线y=$\frac{m-2}{x}$没有交点，那么m的取值范围是m＜2．分析 将y=x代入y=$\frac{m-2}{x}$中整理后即可得出关于x的一元二次方程，由两函数图象无交点即可得知一元二次方程无解，从而得出关于m的一元一次不等式，解之即可得出结论．
解答 解：将y=x代入y=$\frac{m-2}{x}$中，得：x=$\frac{m-2}{x}$，
整理，得：x2=m-2．
∵直线y=x与双曲线y=$\frac{m-2}{x}$没有交点，
∴方程x2=m-2无解，
∴m-2＜0，即m＜2．
故答案为：m＜2．
点评 本题考查了反比例函数与一次函数的交点问题，根据两函数图象无交点找出关于m的一元一次不等式是解题的关键．
练习册系列答案
云南师大附小一线名师提优作业系列答案
相关题目
2．下列说法正确的是（ ）
| A． | -0.64的立方根是-0.4 | B． | 1的平方根是±1 | ||
| C． | 0.4的算术平方根是0.16 | D． | 49的算术平方根是±7 |
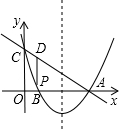如图，抛物线y=x2+bx+c过点A（3，0），B（1，0），交y轴于点C，点P是该抛物线上一动点，点P从点C沿抛物线向A点运动（运动到A点停止），过点P作PD∥y轴交直线AC于点D．
如图，点P是?ABCD边AB上的一点，射线CP交DA的延长线于点E，请从图中找出一对相似三角形：△EAP∽△EDC（答案不唯一）．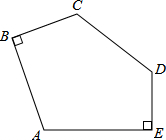
如图，已知AB=CD=AE=BC+DE=4，∠ABC=∠AED=90°，则五边形ABCDE的面积为16．