题目内容
6.已知二次函数y=(x-h)2+1(h为常数),在自变量x的值满足1≤x≤3的情况下,与其对应的函数y的最小值为5,则h的值是( )| A. | -1 | B. | -1或5 | C. | 5 | D. | -5 |
分析 由解析式可知该函数在x=h时取得最小值1、x>h时,y随x的增大而增大、当x<h时,y随x的增大而减小,根据1≤x≤3时,函数的最小值为5可分如下两种情况:①若h<1≤x≤3,x=1时,y取得最小值5;②若1≤x≤3<h,当x=3时,y取得最小值5,分别列出关于h的方程求解即可.
解答 解:∵当x>h时,y随x的增大而增大,当x<h时,y随x的增大而减小,
∴①若h<1≤x≤3,x=1时,y取得最小值5,
可得:(1-h)2+1=5,
解得:h=-1或h=3(舍);
②若1≤x≤3<h,当x=3时,y取得最小值5,
可得:(3-h)2+1=5,
解得:h=5或h=1(舍).
综上,h的值为-1或5,
故选:B.
点评 本题主要考查二次函数的性质和最值,根据二次函数的性质和最值分类讨论是解题的关键.

练习册系列答案
相关题目
14.一元一次不等式2x-3≥-1的解集在数轴上表示为( )
| A. |  | B. |  | C. |  | D. |  |
11.tan60°的值等于( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
18.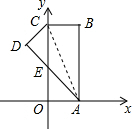 如图,在直角坐标系中,矩形OABC的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E,那么点D的坐标为( )
如图,在直角坐标系中,矩形OABC的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E,那么点D的坐标为( )
 如图,在直角坐标系中,矩形OABC的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E,那么点D的坐标为( )
如图,在直角坐标系中,矩形OABC的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E,那么点D的坐标为( )| A. | (-$\frac{1}{2}$,$\frac{13}{5}$) | B. | (-$\frac{2}{5}$,$\frac{13}{5}$) | C. | (-$\frac{4}{5}$,$\frac{12}{5}$) | D. | (-$\frac{3}{5}$,$\frac{12}{5}$) |
 如图,点P是?ABCD边AB上的一点,射线CP交DA的延长线于点E,请从图中找出一对相似三角形:△EAP∽△EDC(答案不唯一).
如图,点P是?ABCD边AB上的一点,射线CP交DA的延长线于点E,请从图中找出一对相似三角形:△EAP∽△EDC(答案不唯一).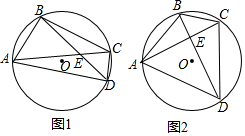 已知:⊙O是四边形ABCD的外接圆,AC与BD交于点E.
已知:⊙O是四边形ABCD的外接圆,AC与BD交于点E.