题目内容
2.解下列方程(1)$\left\{\begin{array}{l}{x+2y+2=0}\\{7x-4y=-41}\end{array}\right.$
(2)$\left\{\begin{array}{l}{\frac{1}{2}x+3y=\frac{2}{3}}\\{x-\frac{3}{4}y=-\frac{29}{12}}\end{array}\right.$.
分析 (1)方程组利用加减消元法求出解即可;
(2)方程组整理后,利用加减消元法求出解即可.
解答 解:方程组整理得:$\left\{\begin{array}{l}{x+2y=-2①}\\{7x-4y=-41②}\end{array}\right.$,
①×2+②得:9x=-45,即x=-5,
把x=-5代入①得:y=$\frac{3}{2}$,
则方程组的解为$\left\{\begin{array}{l}{x=-5}\\{y=\frac{3}{2}}\end{array}\right.$;
(2)方程组整理得:$\left\{\begin{array}{l}{3x+18y=4①}\\{12x-9y=-29②}\end{array}\right.$,
①+②×2得:27x=-54,即x=-2,
把x=-2代入①得:y=$\frac{5}{9}$,
则方程组的解为$\left\{\begin{array}{l}{x=-2}\\{y=\frac{5}{9}}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
相关题目
20.下列变形,正确的是( )
| A. | $\frac{by}{2ay}=\frac{b}{2a}$ | B. | $-\frac{y}{x}=\frac{-y}{-x}$ | ||
| C. | 1+$\frac{1}{a}$=$\frac{2}{a}$ | D. | $\frac{{{a^2}+ab}}{{{b^2}+ab}}=\frac{a^2}{b^2}$ |
12. 张琳同学将某地2016年6月~10月的月降水量绘制成了如图所示的折线统计图,则降雨量变化最大的时间范围是( )
张琳同学将某地2016年6月~10月的月降水量绘制成了如图所示的折线统计图,则降雨量变化最大的时间范围是( )
 张琳同学将某地2016年6月~10月的月降水量绘制成了如图所示的折线统计图,则降雨量变化最大的时间范围是( )
张琳同学将某地2016年6月~10月的月降水量绘制成了如图所示的折线统计图,则降雨量变化最大的时间范围是( )| A. | 6~7月份 | B. | 7~8月份 | C. | 8~9月份 | D. | 9~10月份 |
 直线AB,CD相交于点O,OE平分∠AOD,∠COF=90°,∠BOF=40°,求∠AOC与∠AOE的度数.
直线AB,CD相交于点O,OE平分∠AOD,∠COF=90°,∠BOF=40°,求∠AOC与∠AOE的度数.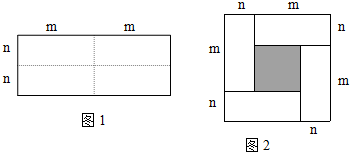
 在我国古算书《周髀算经》中记载周公与商高的谈话,其中就有勾股定理的最早文字记录,即“勾三股四弦五”,亦被称作商高定理.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,∠BAC=90°,AB=3,AC=4,则D,E,F,G,H,I都在矩形KLMJ的边上,那么矩形KLMJ的面积为110.
在我国古算书《周髀算经》中记载周公与商高的谈话,其中就有勾股定理的最早文字记录,即“勾三股四弦五”,亦被称作商高定理.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,∠BAC=90°,AB=3,AC=4,则D,E,F,G,H,I都在矩形KLMJ的边上,那么矩形KLMJ的面积为110.