题目内容
17.如图是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形.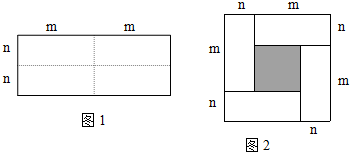
(1)你认为图2中的阴影部分的正方形的边长等于m-n?
(2)请用两种不同的方法求图2中阴影部分的面积.
①(m-n)2
②(m+n)2-4mn
(3)观察图2,请你写出代数式(m+n)2,(m-n)2,mn之间的等量关系(m-n)2=(m+n)2-4mn
根据(3)题中的等量关系,解决下列问题:若a+b=7,ab=5,求(a-b)的值.
分析 (1)根据图形得出即可;
(2)根据图形中各个部分的面积得出即可;
(3)根据(1)中的结果即可得出答案,先根据(2)的结果进行变形,再代入求出即可.
解答 解:(1)图2中的阴影部分的正方形的边长等于m-n,
故答案为:m-n;
(2)图中阴影部分的面积为①(m-n)2或②(m+n)2-4mn,
故答案为:(m-n)2,(m+n)2-4mn;
(3)(m-n)2=(m+n)2-4mn,
∵a+b=7,ab=-5,
∴(a-b)2=(a+b)2-4ab=72-4×(-5)=69,
a-b=±$\sqrt{69}$,
故答案为:(m-n)2=(m+n)2-4mn.
点评 本题考查了完全平方公式的应用,能熟记完全平方公式是解此题的关键,注意:(a+b)2=a2+2ab+b2,(a-b)2=a2-2ab+b2,(a-b)2=(a+b)2-4ab.

练习册系列答案
 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
5.直角三角形两边长分别是3、4,则这个直角三角形的第三边是( )
| A. | 5 | B. | $\sqrt{7}$ | C. | 5或$\sqrt{7}$ | D. | 无法确定 |
9.如果把直角三角形的两条直角边长同时扩大到原来的3倍,那么斜边长扩大到原来的( )
| A. | 3倍 | B. | 4倍 | C. | 6倍 | D. | 9倍 |
7.下列说法正确的是( )
| A. | “若ac=bc,则a=b”是必然事件 | |
| B. | “若|a|+|b|=0,则a=0且b=0”是不确定事件 | |
| C. | “若ab=0,则a=0且b=0”是不可能事件 | |
| D. | “若$\frac{a}{b}$<0,则a>0且b<0”是随机事件 |