题目内容
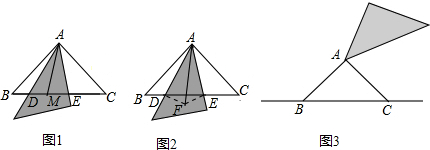
7. 在我国古算书《周髀算经》中记载周公与商高的谈话,其中就有勾股定理的最早文字记录,即“勾三股四弦五”,亦被称作商高定理.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,∠BAC=90°,AB=3,AC=4,则D,E,F,G,H,I都在矩形KLMJ的边上,那么矩形KLMJ的面积为110.
在我国古算书《周髀算经》中记载周公与商高的谈话,其中就有勾股定理的最早文字记录,即“勾三股四弦五”,亦被称作商高定理.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,∠BAC=90°,AB=3,AC=4,则D,E,F,G,H,I都在矩形KLMJ的边上,那么矩形KLMJ的面积为110.
分析 延长AB交KF于点O,延长AC交GM于点P,可得四边形AOLP是正方形,然后求出正方形的边长,再求出矩形KLMJ的长与宽,然后根据矩形的面积公式列式计算即可得解.
解答 解:如图,延长AB交KF于点O,延长AC交GM于点P,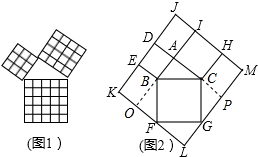
则四边形OALP是矩形.
∵∠CBF=90°,
∴∠ABC+∠OBF=90°,
又∵直角△ABC中,∠ABC+∠ACB=90°,
∴∠OBF=∠ACB,
在△OBF和△ACB中,$\left\{\begin{array}{l}{∠BAC=∠BOF}&{\;}\\{∠ACB=∠OBF}&{\;}\\{BC=BF}&{\;}\end{array}\right.$
∴△OBF≌△ACB(AAS),
∴AC=OB,
同理:△ACB≌△PGC,
∴PC=AB,
∴OA=AP,
∴矩形AOLP是正方形,
边长AO=AB+AC=3+4=7,
∴KL=3+7=10,LM=4+7=11,
∴矩形KLMJ的面积为10×11=110.
点评 本题考查了勾股定理的证明,作出辅助线构造出正方形是解题的关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
5.如图所示的是四个物理实验工具的简图,从左到右依次是小车、弹簧、钩码、三极管,其中是轴对称图形的是( )
| A. |  小车 | B. |  弹簧 | C. |  钩码 | D. |  三极管 |
18.已知$\left\{\begin{array}{l}{x+2y=4k}\\{2x+y=2k+1}\end{array}\right.$且0<y-x<1,则k的取值范围是( )
| A. | -1$<k<-\frac{1}{2}$ | B. | 0$<k<\frac{1}{2}$ | C. | 0<k<1 | D. | $\frac{1}{2}$<k<1 |
16.在平面直角坐标系xOy中,对于点P(a,b)和点Q(a,b′),给出下列定义:若b′=$\left\{\begin{array}{l}{b,}&{a≥1}\\{-b,}&{a<1}\end{array}\right.$,则称点Q为点的限变点.例如:点(2,3)的限变点的坐标是(2,3),点(-2,5)的限变点的坐标是(-2,-5),如果一个点的限变点的坐标是($\sqrt{3}$,-1),那么这个点的坐标是( )
| A. | (-1,$\sqrt{3}$) | B. | (-$\sqrt{3}$,-1) | C. | ($\sqrt{3}$,-1) | D. | ($\sqrt{3}$,1) |