题目内容
9．
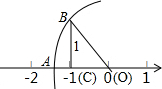如图，直角三角形OBC中，BC=1，OC在数轴上，且点O、C对应的实数分别是0，-1，以点O为圆心，OB的长为半径画弧，与数轴的负半轴交于点A，设点A所对应的实数为x，则x2-10的立方根为（ ）| A． | $\sqrt{2}$-10 | B． | -$\sqrt{2}$-10 | C． | 2 | D． | -2 |
分析 根据勾股定理得出BO的长，进而得出A点对应的数，进而利用立方根的定义得出即可．
解答 解：由题意可得：BC=CO=1，
则BO=$\sqrt{2}$，
故A点对应的实数为：-$\sqrt{2}$，
则x2-10=（-$\sqrt{2}$）2-10=-8，
故x2-10的立方根为：-2．
故选：D．
点评 此题主要考查了实数与数轴，根据题意得出x的值是解题关键．
练习册系列答案
浙江新课程三维目标测评课时特训系列答案
周周清检测系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
19．
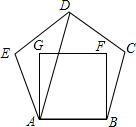把边长相等的正五边形ABCDE和正方形ABFG，按照如图所示的方式叠合在一起，连结AD，则∠DAG=（ ）
把边长相等的正五边形ABCDE和正方形ABFG，按照如图所示的方式叠合在一起，连结AD，则∠DAG=（ ）| A． | 18° | B． | 20° | C． | 28° | D． | 30° |
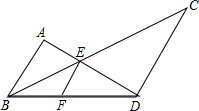如图，AB∥EF∥CD，E为AD与BC的交点，F在BD上，求证：$\frac{1}{AB}$+$\frac{1}{CD}$=$\frac{1}{EF}$．
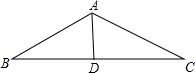如图，在△ABC中，AB=17，BC=30，BC边上的中线AD=8，∠B与∠C相等吗？
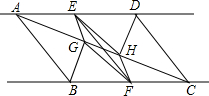如图，已知直线m∥n，A，D两点在直线m上，B，C两点在直线n上，且AB∥CD，E，F分别是AD，BC的中点，BG⊥AC，DH⊥AC，点G，H分别是垂足．求证：EF与GH互相平分．
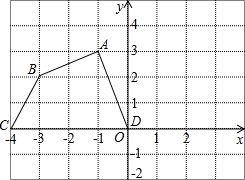如图，在平面直角坐标系中，四边形ABCD各个顶点的坐标分别为A（-1，3），B（-3，2），C（-4，0），D（0，0）