题目内容
1.某物资站新进60吨散装竹炭,为了获取更多的利润,该物资站决定将其包装后再出售,根据市场调查,该物资站决定将其包装成3吨和2吨两种包装(货物要全部包装,不留余货),其中3吨装和2吨装的包装成本分别是80元/件和60元/件,2吨包装的竹炭总量不少于40吨.(1)若该物资站要求包装成本不少于1700元,但又不多于1800元,则该物资站有几种不同的包装方案?
(2)在(1)的条件下,怎样设计包装方案才能使包装成本最低?最低成本是多少元?
(3)在(1)的条件下,除去各项成本后,若每个2吨包装的竹炭售出后可获利a元(a为整数),每个3吨包装的竹炭售出后可获利270元,全部售出后,共获利5940元,则按哪种包装方案,并求出对应的a的值.
分析 (1)首先用未知数表示出包装为2吨的件数,然后根据两种包装的总重量为60吨,来表示出包装为3吨的件数;然后根据“包装成本不少于1700元,但又不多于1800元”以及“2吨包装的货物总量不少于40吨”,列出不等式组,求出未知数的取值范围,由于件数必须使正整数,可据此求出x的整数值,从而确定出有几种包装方案.
(2)根据(1)得到的包装方案以及题目给出的各种包装的单件成本,列式求出各种方案所需成本,即可得到包装成本最低的方案以及成本的最低值.
(3)根据(1)得到的包装为2吨、3吨的件数表达式,结合各种包装的单件获利额,即可表示出两种包装总的获利额,由此得关于总的获利额和(1)所设未知数的函数关系式,根据函数的性质即可确定出获利最多的包装方案.
解答 解:(1)设2吨装x件,3吨装的$\frac{60-2x}{3}$件
由题意,得$\left\{\begin{array}{l}{1700≤60x+\frac{60-2x}{3}×80≤1800}\\{2x≥40}\end{array}\right.$,
解得,20≤x≤30,∵$\frac{60-2x}{3}$是正整数,
∴有三种包装方案:
①x=21,y=6,②x=24,y=4,③x=27,y=2.
(2)∵21×60+6×80=1740,
24×60+4×80=1760,
27×60+2×80=1780,
∴2吨装21件,3吨装6件成本最低,最低成本1740元.
(3)设利润为W元,$W=200a+270×\frac{60-2a}{3}$=20a+5400;
∴当a=27时,W最大=20×27+5400=5940;
答:应用方案③:2吨装27件,3吨装2件获利最大,此时a的值是27.
点评 此题主要考查了一次函数的应用,关键是根据一元一次不等式组的实际应用以及一次函数最值的应用分析.

 导学全程练创优训练系列答案
导学全程练创优训练系列答案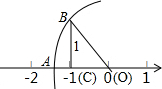 如图,直角三角形OBC中,BC=1,OC在数轴上,且点O、C对应的实数分别是0,-1,以点O为圆心,OB的长为半径画弧,与数轴的负半轴交于点A,设点A所对应的实数为x,则x2-10的立方根为( )
如图,直角三角形OBC中,BC=1,OC在数轴上,且点O、C对应的实数分别是0,-1,以点O为圆心,OB的长为半径画弧,与数轴的负半轴交于点A,设点A所对应的实数为x,则x2-10的立方根为( )| A. | $\sqrt{2}$-10 | B. | -$\sqrt{2}$-10 | C. | 2 | D. | -2 |
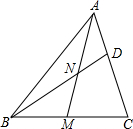 如图所示,在△ABC中,AM是中线,N是AM的中点,BN的延长线交AC于点D,若AC=12,求CD的长.
如图所示,在△ABC中,AM是中线,N是AM的中点,BN的延长线交AC于点D,若AC=12,求CD的长.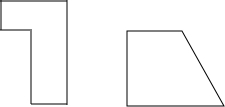 某公园准备用如图所示的材料给一块矩形的场地铺地面
某公园准备用如图所示的材料给一块矩形的场地铺地面