题目内容
20.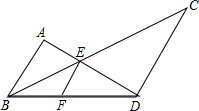 如图,AB∥EF∥CD,E为AD与BC的交点,F在BD上,求证:$\frac{1}{AB}$+$\frac{1}{CD}$=$\frac{1}{EF}$.
如图,AB∥EF∥CD,E为AD与BC的交点,F在BD上,求证:$\frac{1}{AB}$+$\frac{1}{CD}$=$\frac{1}{EF}$.
分析 根据平行线分线段成比例定理,得到$\frac{EF}{AB}$=$\frac{DF}{DB}$和$\frac{EF}{CD}$=$\frac{BF}{BD}$,求和化简得到答案.
解答 解:∵AB∥EF,
∴$\frac{EF}{AB}$=$\frac{DF}{DB}$,
∵EF∥CD,
∴$\frac{EF}{CD}$=$\frac{BF}{BD}$,
∴$\frac{EF}{AB}$+$\frac{EF}{CD}$=$\frac{DF}{DB}$+$\frac{BF}{BD}$=1,
∴$\frac{1}{AB}$+$\frac{1}{CD}$=$\frac{1}{EF}$.
点评 本题考查的是平行线分线段成比例定理,掌握定理、找准对应关系是解题的关键.

练习册系列答案
相关题目
9.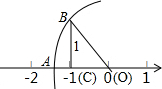 如图,直角三角形OBC中,BC=1,OC在数轴上,且点O、C对应的实数分别是0,-1,以点O为圆心,OB的长为半径画弧,与数轴的负半轴交于点A,设点A所对应的实数为x,则x2-10的立方根为( )
如图,直角三角形OBC中,BC=1,OC在数轴上,且点O、C对应的实数分别是0,-1,以点O为圆心,OB的长为半径画弧,与数轴的负半轴交于点A,设点A所对应的实数为x,则x2-10的立方根为( )
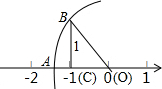 如图,直角三角形OBC中,BC=1,OC在数轴上,且点O、C对应的实数分别是0,-1,以点O为圆心,OB的长为半径画弧,与数轴的负半轴交于点A,设点A所对应的实数为x,则x2-10的立方根为( )
如图,直角三角形OBC中,BC=1,OC在数轴上,且点O、C对应的实数分别是0,-1,以点O为圆心,OB的长为半径画弧,与数轴的负半轴交于点A,设点A所对应的实数为x,则x2-10的立方根为( )| A. | $\sqrt{2}$-10 | B. | -$\sqrt{2}$-10 | C. | 2 | D. | -2 |
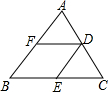 如图,△ABC中,D是AC的中点,DF∥BC,交AB于F,DE∥AB,交BC于E,试判断:AF与DE,CE与DF的长度之间有什么关系?请说明理由.
如图,△ABC中,D是AC的中点,DF∥BC,交AB于F,DE∥AB,交BC于E,试判断:AF与DE,CE与DF的长度之间有什么关系?请说明理由.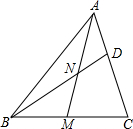 如图所示,在△ABC中,AM是中线,N是AM的中点,BN的延长线交AC于点D,若AC=12,求CD的长.
如图所示,在△ABC中,AM是中线,N是AM的中点,BN的延长线交AC于点D,若AC=12,求CD的长.