题目内容
14.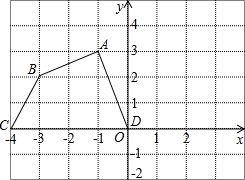 如图,在平面直角坐标系中,四边形ABCD各个顶点的坐标分别为A(-1,3),B(-3,2),C(-4,0),D(0,0)
如图,在平面直角坐标系中,四边形ABCD各个顶点的坐标分别为A(-1,3),B(-3,2),C(-4,0),D(0,0)(1)求四边形ABCD的面积;
(2)如果把四边形ABCD各个顶点的横坐标加2,纵坐标减1,所得四边形的面积又是多少?试画出四边形.
分析 (1)把四边形ABCD分割为两个三角形和一个直角梯形,然后根据三角形面积公式和梯形的面积公式进行计算;
(2)由于把四边形ABCD各个顶点的横坐标加2,纵坐标减1,则相当于把四边形四边形ABCD向右平移2个单位,再向下平移1个单位,利用平移的性质得到平移后的四边形的面积不变.
解答 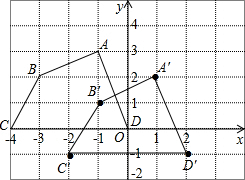 解:(1)四边形ABCD的面积=$\frac{1}{2}$×1×2+$\frac{1}{2}$×(2+3)×2+$\frac{1}{2}$×1×3=$\frac{15}{2}$;
解:(1)四边形ABCD的面积=$\frac{1}{2}$×1×2+$\frac{1}{2}$×(2+3)×2+$\frac{1}{2}$×1×3=$\frac{15}{2}$;
(2)把四边形ABCD各个顶点的横坐标加2,纵坐标减1,所得四边形的面积与原四边形的面积相等,为$\frac{15}{2}$,
如图,四边形A′B′C′D′为所求.
点评 本题考查了坐标与图形性质:利用点的坐标计算相应线段的长和判断线段与坐标轴的位置关系.也考查了三角形面积公式.

练习册系列答案
相关题目
4.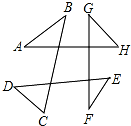 如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H的度数为( )
如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H的度数为( )
 如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H的度数为( )
如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H的度数为( )| A. | 90° | B. | 180° | C. | 270° | D. | 360° |
9.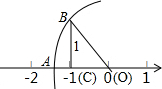 如图,直角三角形OBC中,BC=1,OC在数轴上,且点O、C对应的实数分别是0,-1,以点O为圆心,OB的长为半径画弧,与数轴的负半轴交于点A,设点A所对应的实数为x,则x2-10的立方根为( )
如图,直角三角形OBC中,BC=1,OC在数轴上,且点O、C对应的实数分别是0,-1,以点O为圆心,OB的长为半径画弧,与数轴的负半轴交于点A,设点A所对应的实数为x,则x2-10的立方根为( )
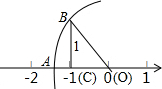 如图,直角三角形OBC中,BC=1,OC在数轴上,且点O、C对应的实数分别是0,-1,以点O为圆心,OB的长为半径画弧,与数轴的负半轴交于点A,设点A所对应的实数为x,则x2-10的立方根为( )
如图,直角三角形OBC中,BC=1,OC在数轴上,且点O、C对应的实数分别是0,-1,以点O为圆心,OB的长为半径画弧,与数轴的负半轴交于点A,设点A所对应的实数为x,则x2-10的立方根为( )| A. | $\sqrt{2}$-10 | B. | -$\sqrt{2}$-10 | C. | 2 | D. | -2 |
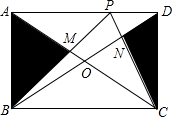 如图所示,矩形ABCD的面积为36平方厘米,四边形PMON的面积是3平方厘米,则阴影部分的面积是12平方厘米.
如图所示,矩形ABCD的面积为36平方厘米,四边形PMON的面积是3平方厘米,则阴影部分的面积是12平方厘米.