题目内容
9.某商场统计了去年1~5月A,B两种品牌冰箱的销售情况.| A品牌(台) | 15 | 17 | 16 | 13 | 14 |
| B品牌(台) | 10 | 14 | 15 | 16 | 20 |
分析 先利用方差公式分别计算出A、B品牌的方差,然后根据方差的意义判断这两种品牌冰箱月销售量的稳定性.
解答 解:A品牌的销售量的平均数为$\frac{15+17+16+13+14}{5}$=15,
B品牌的销售量的平均数为$\frac{10+14+15+16+20}{5}$=15,
A品牌的方差=$\frac{1}{5}$[(13-15)2+(14-15)2+(15-15)2+(16-15)2+[(17-15)2]=2,
B品牌的方差=$\frac{1}{5}$[(10-15)2+(14-15)2+(15-15)2+(16-15)2+[(20-15)2]=10.4,
因为10.4>2,所以A品牌的销售量较为稳定A,
故答案为A.
点评 本题考查了方差,一般地设n个数据,x1,x2,…xn的平均数为$\overline{x}$,则方差S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.

练习册系列答案
相关题目
17.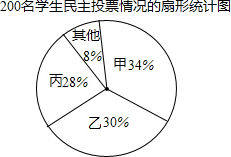 某校九年级有200名学生,为了向市团委推荐本年级一名学生参加团代会,按如下程序进行了民主投票,推荐的程序是:首先由全年级学生对六名候选人进行投票,每名学生只能给一名候选人投票,选出票数多的前三名;然后再对这三名候选人(记为甲、乙、丙)进行笔试和面试,两个程序的结果统计如下:
某校九年级有200名学生,为了向市团委推荐本年级一名学生参加团代会,按如下程序进行了民主投票,推荐的程序是:首先由全年级学生对六名候选人进行投票,每名学生只能给一名候选人投票,选出票数多的前三名;然后再对这三名候选人(记为甲、乙、丙)进行笔试和面试,两个程序的结果统计如下:
请你根据以上信息解答下列问题:
(1)请分别计算甲、乙、丙的得票数;
(2)若规定每名候选人得一票记1分,将投票、笔试、面试三项得分按照2:5:3的比例计入每名候选人的总成绩,成绩最高的将被推荐,请通过计算说明甲、乙、丙哪名学生将被推荐.
 某校九年级有200名学生,为了向市团委推荐本年级一名学生参加团代会,按如下程序进行了民主投票,推荐的程序是:首先由全年级学生对六名候选人进行投票,每名学生只能给一名候选人投票,选出票数多的前三名;然后再对这三名候选人(记为甲、乙、丙)进行笔试和面试,两个程序的结果统计如下:
某校九年级有200名学生,为了向市团委推荐本年级一名学生参加团代会,按如下程序进行了民主投票,推荐的程序是:首先由全年级学生对六名候选人进行投票,每名学生只能给一名候选人投票,选出票数多的前三名;然后再对这三名候选人(记为甲、乙、丙)进行笔试和面试,两个程序的结果统计如下:| 试项目 | 测试成绩/分 | ||
| 甲 | 乙 | 丙 | |
| 笔试 | 92 | 90 | 95 |
| 面试 | 85 | 95 | 80 |
(1)请分别计算甲、乙、丙的得票数;
(2)若规定每名候选人得一票记1分,将投票、笔试、面试三项得分按照2:5:3的比例计入每名候选人的总成绩,成绩最高的将被推荐,请通过计算说明甲、乙、丙哪名学生将被推荐.
14. 今年3月12日是我国第38个义务植树节,为绿化家园,拟选去年栽种的A、B、C三种品种中成活率最高的进行栽种,统计三种树的成活情况如表,并把成活的棵数绘制成如下不完整的统计图.
今年3月12日是我国第38个义务植树节,为绿化家园,拟选去年栽种的A、B、C三种品种中成活率最高的进行栽种,统计三种树的成活情况如表,并把成活的棵数绘制成如下不完整的统计图.
(1)B种树苗成活了多少棵?并补全条形统计图;
(2)若明年B种树苗要成活3000棵,则今年植树节需种B种树苗至少几棵?
 今年3月12日是我国第38个义务植树节,为绿化家园,拟选去年栽种的A、B、C三种品种中成活率最高的进行栽种,统计三种树的成活情况如表,并把成活的棵数绘制成如下不完整的统计图.
今年3月12日是我国第38个义务植树节,为绿化家园,拟选去年栽种的A、B、C三种品种中成活率最高的进行栽种,统计三种树的成活情况如表,并把成活的棵数绘制成如下不完整的统计图.(1)B种树苗成活了多少棵?并补全条形统计图;
(2)若明年B种树苗要成活3000棵,则今年植树节需种B种树苗至少几棵?
| 品种 | 今年成活棵树 | 成活率 |
| A | 540 | 90% |
| B | a | 96% |
| C | 368 | 92% |
| 合计 | 1388 |
18.下列计算中正确的是( )
| A. | -1-1=0 | B. | 32=6 | C. | -2÷$\frac{1}{2}$=-1 | D. | -33-(-3)3=0 |
19. 六个函数分别是①y=x;②y=-x+1;③y=x2;④y=-x2+2x-1;⑤y=x3;⑥y=-x3+1.
六个函数分别是①y=x;②y=-x+1;③y=x2;④y=-x2+2x-1;⑤y=x3;⑥y=-x3+1.
(1)其中一次函数是①,②,二次函数是③,④,则⑤,⑥的函数可以定义为三次函数;
(2)我们可以借鉴以前研究函数的经验,先探索函数y=x3的图象和性质;
①填写下表,画出函数的图象;
②观察图象,写出该函数两条不同类型的性质;
(3)若点A(a,b)(a>0)是函数y=x3图象上一点,点A关于y轴的对称点为点B,点A关于原点O的对称点为点C,若顺次连接A,B,C,则△ABC的形状为直角三角形;
(4)函数y=-x3+1的图象关于点(0,1)成中心对称图形.
 六个函数分别是①y=x;②y=-x+1;③y=x2;④y=-x2+2x-1;⑤y=x3;⑥y=-x3+1.
六个函数分别是①y=x;②y=-x+1;③y=x2;④y=-x2+2x-1;⑤y=x3;⑥y=-x3+1.(1)其中一次函数是①,②,二次函数是③,④,则⑤,⑥的函数可以定义为三次函数;
(2)我们可以借鉴以前研究函数的经验,先探索函数y=x3的图象和性质;
①填写下表,画出函数的图象;
②观察图象,写出该函数两条不同类型的性质;
| x | … | -2 | -$\frac{3}{2}$ | -1 | 0 | 1 | $\frac{3}{2}$ | 2 | … |
| y=x3 | … | … |
(4)函数y=-x3+1的图象关于点(0,1)成中心对称图形.
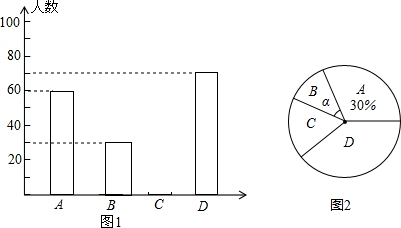 黔东南州某中学为了解本校学生平均每天的课外学习实践情况,随机抽取部分学生进行问卷调查,并将调查结果分为A,B,C,D四个等级,设学生时间为t(小时),A:t<1,B:1≤t<1.5,C:1.5≤t<2,D:t≥2,根据调查结果绘制了如图所示的两幅不完整的统计图.请你根据图中信息解答下列问题:
黔东南州某中学为了解本校学生平均每天的课外学习实践情况,随机抽取部分学生进行问卷调查,并将调查结果分为A,B,C,D四个等级,设学生时间为t(小时),A:t<1,B:1≤t<1.5,C:1.5≤t<2,D:t≥2,根据调查结果绘制了如图所示的两幅不完整的统计图.请你根据图中信息解答下列问题: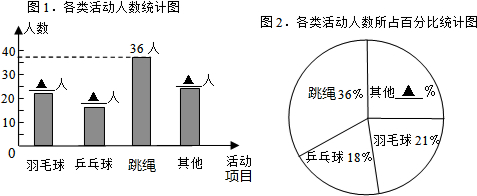
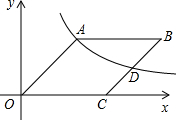 如图,O为坐标原点,点C在x轴的正半轴上,四边形OABC是平行四边形,∠AOC=45°,OA=2,反比例函数y=$\frac{k}{x}$在第一现象内的图象经过点A,与BC交于点D.
如图,O为坐标原点,点C在x轴的正半轴上,四边形OABC是平行四边形,∠AOC=45°,OA=2,反比例函数y=$\frac{k}{x}$在第一现象内的图象经过点A,与BC交于点D.