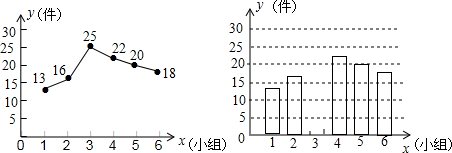
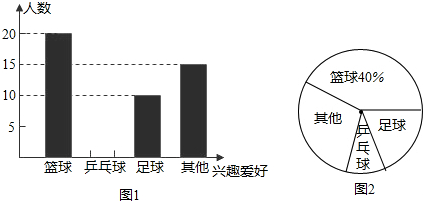
题目内容
10.在徒骇河观景堤坝上有一段斜坡,为了方便游客通行,现准备铺上台阶,某施工队测得斜坡上铅锤的两棵树间水平距离AB=4米,斜坡距离BC=4.25米,斜坡总长DE=85米.(1)求坡角∠D的度数(结果精确到1°)
(2)若这段斜坡用厚度为15cm的长方体台阶来铺,需要铺几级台阶?(最后一个高不足15cm时,按一个台阶计算)
(参考数据:cos20°≈0.94,sin20°≈0.34,sin18°≈0.31,cos18°≈0.95)

分析 (1)利用余弦的定义求出∠ABC的度数,根据平行线的性质得到答案;
(2)利用正弦的定义求出EF的长,根据题意计算即可.
解答 解:(1)cos∠ABC=$\frac{AB}{BC}$≈0.94,
∴∠ABC≈20°,
由题意得,∠D=∠ABC≈20°;
(2)EF=DE•sin∠D=85×0.34=28.9米,
28.9×100÷15≈193,
答:需要铺193级台阶.
点评 本题考查的是解直角三角形的应用-坡度坡角问题,熟记锐角三角函数的定义、掌握坡度的概念是解题的关键.

练习册系列答案
相关题目
18.下列计算中正确的是( )
| A. | -1-1=0 | B. | 32=6 | C. | -2÷$\frac{1}{2}$=-1 | D. | -33-(-3)3=0 |
19.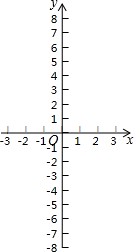 六个函数分别是①y=x;②y=-x+1;③y=x2;④y=-x2+2x-1;⑤y=x3;⑥y=-x3+1.
六个函数分别是①y=x;②y=-x+1;③y=x2;④y=-x2+2x-1;⑤y=x3;⑥y=-x3+1.
(1)其中一次函数是①,②,二次函数是③,④,则⑤,⑥的函数可以定义为三次函数;
(2)我们可以借鉴以前研究函数的经验,先探索函数y=x3的图象和性质;
①填写下表,画出函数的图象;
②观察图象,写出该函数两条不同类型的性质;
(3)若点A(a,b)(a>0)是函数y=x3图象上一点,点A关于y轴的对称点为点B,点A关于原点O的对称点为点C,若顺次连接A,B,C,则△ABC的形状为直角三角形;
(4)函数y=-x3+1的图象关于点(0,1)成中心对称图形.
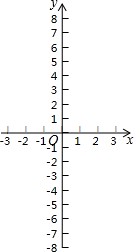 六个函数分别是①y=x;②y=-x+1;③y=x2;④y=-x2+2x-1;⑤y=x3;⑥y=-x3+1.
六个函数分别是①y=x;②y=-x+1;③y=x2;④y=-x2+2x-1;⑤y=x3;⑥y=-x3+1.(1)其中一次函数是①,②,二次函数是③,④,则⑤,⑥的函数可以定义为三次函数;
(2)我们可以借鉴以前研究函数的经验,先探索函数y=x3的图象和性质;
①填写下表,画出函数的图象;
②观察图象,写出该函数两条不同类型的性质;
| x | … | -2 | -$\frac{3}{2}$ | -1 | 0 | 1 | $\frac{3}{2}$ | 2 | … |
| y=x3 | … | … |
(4)函数y=-x3+1的图象关于点(0,1)成中心对称图形.
20.下列图形是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
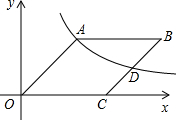 如图,O为坐标原点,点C在x轴的正半轴上,四边形OABC是平行四边形,∠AOC=45°,OA=2,反比例函数y=$\frac{k}{x}$在第一现象内的图象经过点A,与BC交于点D.
如图,O为坐标原点,点C在x轴的正半轴上,四边形OABC是平行四边形,∠AOC=45°,OA=2,反比例函数y=$\frac{k}{x}$在第一现象内的图象经过点A,与BC交于点D.