题目内容
20.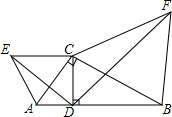 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,分别以AC,BC为边向三角形外作等边△ACE和等边△BCF,连接DE,DF,试说明:△ADE∽△CDF.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,分别以AC,BC为边向三角形外作等边△ACE和等边△BCF,连接DE,DF,试说明:△ADE∽△CDF.
分析 先利用等角的余角相等得到∠CAD=∠BCD,则利用有两组角对应相等的两个三角形相似可判断Rt△ACD∽Rt△CBD,得到$\frac{AC}{BC}$=$\frac{AD}{CD}$,再根据等边三角形的性质得AE=AC,CF=CB,∠EAC=60°,∠FCB=60°,则$\frac{AE}{CF}$=$\frac{AD}{CD}$,接着证明∠EAD=∠FCD,然后根据两组对应边的比相等且夹角对应相等的两个三角形相似可判断△ADE∽△CDF.
解答 证明:∵∠ACB=90°,CD⊥AB,
∴∠CAD=∠BCD,
∴Rt△ACD∽Rt△CBD,
∴$\frac{AC}{BC}$=$\frac{AD}{CD}$,
∵△ACE和△BCF都为等边三角形,
∴AE=AC,CF=CB,∠EAC=60°,∠FCB=60°,
∴$\frac{AE}{CF}$=$\frac{AD}{CD}$,
∵∠EAD=∠EAC+∠CAD=60°+∠CAD,∠DCF=∠BCF+∠BCD=60°+∠BCD,
∴∠EAD=∠FCD,
∴△ADE∽△CDF.
点评 本题考查了相似三角形的判定:两组对应边的比相等且夹角对应相等的两个三角形相似;有两组角对应相等的两个三角形相似.也考查了等边三角形的性质.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目