题目内容
15.a,b,c分别为△ABC的三边,且满足a+b=3c-2,a-b=2c-6.(1)求c的取值范围;
(2)若△ABC的周长为18,求c的值.
分析 (1)根据三角形任意两边之和大于第三边得出3c-2>c,任意两边之差小于第三边得出|2c-6|<c,列不等式组求解即可;
(2)由△ABC的周长为18,a+b=3c-2,4c-2=18,解方程得出答案即可.
解答 解:(1)∵a,b,c分别为△ABC的三边,a+b=3c-2,a-b=2c-6,
∴$\left\{\begin{array}{l}{3c-2>c}\\{|2c-6|<c}\end{array}\right.$,
解得:2<c<6;
(2)∵△ABC的周长为18,a+b=3c-2,
∴a+b+c=4c-2=18,
解得c=5.
点评 此题考查三角形的三边关系,利用三角形任意两边之和大于第三边,任意两边之差小于第三边,建立不等式解决问题.

练习册系列答案
相关题目
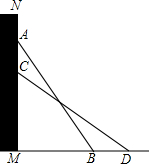 如图,把一个长为10m的梯子AB斜靠在墙上,测得AM=8m,BM=6m,梯子沿墙下滑到CD位置,测得∠ABM=∠DCM,求梯子下滑的高度.
如图,把一个长为10m的梯子AB斜靠在墙上,测得AM=8m,BM=6m,梯子沿墙下滑到CD位置,测得∠ABM=∠DCM,求梯子下滑的高度.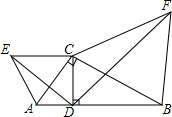 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,分别以AC,BC为边向三角形外作等边△ACE和等边△BCF,连接DE,DF,试说明:△ADE∽△CDF.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,分别以AC,BC为边向三角形外作等边△ACE和等边△BCF,连接DE,DF,试说明:△ADE∽△CDF.