题目内容
10.小红在课外活动时,不小心把老师用的三角形教具弄坏了一个角,如图①所示,她想用一块同样材料的薄板把它补上,想出以下办法:(1)先量出∠AED,∠BDE的度数,量出DE的长;(2)在同样的材料上取D1E1=DE,用量角器∠ME1D1=180°-∠AED″,∠ND1E1=180°-∠BDE,如图②所示,两射线E1M,D1N交于点C1,剪下△C1D1E1,将其与原三角形黏合就能把三角形教具修好,你认为这两种方法可行吗?道理是什么?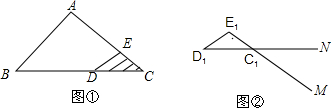
分析 利用全等三角形的判定定理ASA证得△C1D1E1≌△CDE即可.
解答 解:这个方法可行,理由如下:
∵∠ME1D1=180°-∠AED,∠ND1E1=180°-∠BDE,
∴∠ME1D1=∠CED,∠ND1E1=∠CDE,
∴在△C1D1E1与△CDE中,$\left\{\begin{array}{l}{∠M{E}_{1}{D}_{1}=∠CED}\\{{D}_{1}{E}_{1}=DE}\\{∠N{D}_{1}{E}_{1}=∠CDE}\end{array}\right.$,
∴△C1D1E1≌△CDE(ASA),
∴该方法可行.
点评 本题考查了全等三角形的应用.在实际生活中,对于难以实地测量的线段,常常通过两个全等三角形,转化需要测量的线段到易测量的边上或者已知边上来,从而求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.计算-$\frac{2}{5}$+($\frac{5}{8}$$-\frac{1}{6}$$+\frac{7}{12}$)×(-2.4)的结果是( )
| A. | -2.9 | B. | 2.9 | C. | -2.8 | D. | 2.8 |
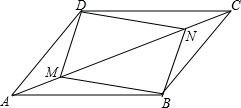 已知:如图,在平行四边形ABCD中,点M,N在对角线AC上,且AM=CN.求证:四边形BMDN是平行四边形.
已知:如图,在平行四边形ABCD中,点M,N在对角线AC上,且AM=CN.求证:四边形BMDN是平行四边形. 如图,已知∠1=∠2,DE=CE,∠AEB=90°,求证:∠3=∠4.
如图,已知∠1=∠2,DE=CE,∠AEB=90°,求证:∠3=∠4. 如图所示,M是梯形ABCD的腰CD的中点,MN⊥AB,垂足为N.求证:S△ABM=$\frac{1}{2}$梯形ABCD.
如图所示,M是梯形ABCD的腰CD的中点,MN⊥AB,垂足为N.求证:S△ABM=$\frac{1}{2}$梯形ABCD.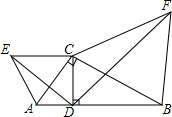 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,分别以AC,BC为边向三角形外作等边△ACE和等边△BCF,连接DE,DF,试说明:△ADE∽△CDF.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,分别以AC,BC为边向三角形外作等边△ACE和等边△BCF,连接DE,DF,试说明:△ADE∽△CDF.