题目内容
12.在等腰△ABC中,∠ABC=∠C=40°,延长AB至点D,使AD=BC,求∠BCD的度数.分析 根据题意画出图形,由等腰三角形的性质求出∠BAC的度数,再以BC为一边在△ABC外作等边△BCE,连接AE,证△ABE和△ACE全等,得到∠CEA=∠BEA=30°,再证△ACE和△CAD全等,推出∠D的度数,根据三角形的内角和定理求出∠ACD,即可求出答案.
解答 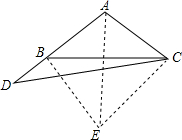 解:如图所示,∵在等腰△ABC中,∠ABC=∠C=40°,
解:如图所示,∵在等腰△ABC中,∠ABC=∠C=40°,
∴∠BAC=180°-40°-40°=100°.
以BC为一边在△ABC外作等边△BCE,连接AE,
∴BE=CE=BC,∠BEC=∠BCE=60°,
在△ABE与△ACE中,
∵$\left\{\begin{array}{l}AB=AC\\ AE=AE\\ BE=CE\end{array}\right.$
∴△ABE≌△ACE(SSS),
∴∠CEA=∠BEA=$\frac{1}{2}$×60°=30°,
∵∠BAC=100°,
∴∠ABC=∠ACB=40°,
∴∠ACE=∠CAD=100°,
在△ACE与△CAD中,
∵$\left\{\begin{array}{l}AD=CE\\∠ACE=∠CAD\\ AC=AC\end{array}\right.$
∴△ACE≌△CAD(SAS),
∴∠D=∠CEA=30°,
在△ACD中,∠ACD=180°-∠D-∠A=50°,
∴∠BCD=∠ACD-∠ACB=10°.
点评 本题主要考查了等腰三角形的性质,全等三角形的性质和判定等知识点,作辅助线和证两个三角形全等是解此题的关键.难点是辅助线的作法.

练习册系列答案
相关题目
2.计算-$\frac{2}{5}$+($\frac{5}{8}$$-\frac{1}{6}$$+\frac{7}{12}$)×(-2.4)的结果是( )
| A. | -2.9 | B. | 2.9 | C. | -2.8 | D. | 2.8 |
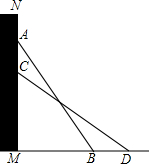 如图,把一个长为10m的梯子AB斜靠在墙上,测得AM=8m,BM=6m,梯子沿墙下滑到CD位置,测得∠ABM=∠DCM,求梯子下滑的高度.
如图,把一个长为10m的梯子AB斜靠在墙上,测得AM=8m,BM=6m,梯子沿墙下滑到CD位置,测得∠ABM=∠DCM,求梯子下滑的高度.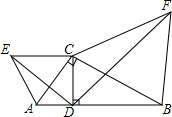 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,分别以AC,BC为边向三角形外作等边△ACE和等边△BCF,连接DE,DF,试说明:△ADE∽△CDF.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,分别以AC,BC为边向三角形外作等边△ACE和等边△BCF,连接DE,DF,试说明:△ADE∽△CDF. 设有两个非负数a、b.则有如下证明:∵($\sqrt{a}$-$\sqrt{b}$)2≥0(当且仅当a=b时等号成立).∴a-2$\sqrt{ab}$+b≥0.∴a+b≥2$\sqrt{ab}$,∴$\sqrt{ab}$≤$\frac{a+b}{2}$(或ab≤$\frac{(a+b)^{2}}{4}$)(当且仅当a=b时等号成立)根据这一证明的结论解答下列问题:
设有两个非负数a、b.则有如下证明:∵($\sqrt{a}$-$\sqrt{b}$)2≥0(当且仅当a=b时等号成立).∴a-2$\sqrt{ab}$+b≥0.∴a+b≥2$\sqrt{ab}$,∴$\sqrt{ab}$≤$\frac{a+b}{2}$(或ab≤$\frac{(a+b)^{2}}{4}$)(当且仅当a=b时等号成立)根据这一证明的结论解答下列问题: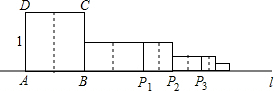 如图,正方形ABCD的边长为1,AB边与直线l重合,沿AB边的中垂线将正方形剪开,剪开后的右侧部分以B为中心,顺时针旋转90°,得到以BP1为边的新矩形,我们称之为第1次操作;沿BP1边的中垂线将矩形剪开,再将剪开后的右侧部分以点P1为中心,顺时针旋转90°,得到以P1P2为边的正方形,我们称之为第2次操作…按此规律继续操作下去,AP2016的长为AP2016=$\frac{{2}^{1010}-3}{{2}^{1008}}$.
如图,正方形ABCD的边长为1,AB边与直线l重合,沿AB边的中垂线将正方形剪开,剪开后的右侧部分以B为中心,顺时针旋转90°,得到以BP1为边的新矩形,我们称之为第1次操作;沿BP1边的中垂线将矩形剪开,再将剪开后的右侧部分以点P1为中心,顺时针旋转90°,得到以P1P2为边的正方形,我们称之为第2次操作…按此规律继续操作下去,AP2016的长为AP2016=$\frac{{2}^{1010}-3}{{2}^{1008}}$.