题目内容
5.关于x的方程kx2-(3k-1)x+2(k-1)=0.(1)求证:无论k为何实数,方程总有实数根;
(2)若此方程有两个实数根x1、x2,且x1+x2-x1x2 =2,求k的值.
分析 (1)分两种情况讨论:①当k=0时,方程是一元一次方程,有实数根;②当k≠0时,方程是一元二次方程,所以证明判别式是非负数即可;
(2)先根据根与系数的关系表示出x1+x2,x1x2,再代入方程求关于k的方程即可.
解答 (1)证明:①当k=0时,x-2=0,得x=2,有实数根;
②当k≠0时,方程是一元二次方程,
∵△=(3k-1)2-4k×2(k-1)=(k+1)2≥0,
∴无论k为何实数,方程总有实数根;
综上所述,无论k为何实数,方程总有实数根;
(2)解:∵方程有两个实数根,
∴k≠0,方程为一元二次方程.
由已知可得x1+x2=$\frac{3k-1}{k}$,x1x2 =$\frac{2(k-1)}{k}$,
∵x1+x2-x1x2 =2,
∴$\frac{3k-1}{k}$-$\frac{2(k-1)}{k}$=2,
∴k=1.
点评 本题主要考查一元二次方程根的判别式和根与系数的关系的应用,同时考查了学生的综合应用能力及推理能力.

练习册系列答案
相关题目
14.某商场经销一种商品,由于进货时价格比原进价降低了5%,使得利润率增加了6个百分点,那么经销这种商品原来的利润是( )
| A. | 14% | B. | 15% | C. | 16% | D. | 17% |
 如图,已知∠1=∠2,DE=CE,∠AEB=90°,求证:∠3=∠4.
如图,已知∠1=∠2,DE=CE,∠AEB=90°,求证:∠3=∠4. 如图,△ABC中,D是AB中点,E是AC上的点,且3AE=2AC,CD,BE交于O点,求证:OE=$\frac{1}{4}$BE.
如图,△ABC中,D是AB中点,E是AC上的点,且3AE=2AC,CD,BE交于O点,求证:OE=$\frac{1}{4}$BE.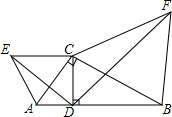 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,分别以AC,BC为边向三角形外作等边△ACE和等边△BCF,连接DE,DF,试说明:△ADE∽△CDF.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,分别以AC,BC为边向三角形外作等边△ACE和等边△BCF,连接DE,DF,试说明:△ADE∽△CDF. 设有两个非负数a、b.则有如下证明:∵($\sqrt{a}$-$\sqrt{b}$)2≥0(当且仅当a=b时等号成立).∴a-2$\sqrt{ab}$+b≥0.∴a+b≥2$\sqrt{ab}$,∴$\sqrt{ab}$≤$\frac{a+b}{2}$(或ab≤$\frac{(a+b)^{2}}{4}$)(当且仅当a=b时等号成立)根据这一证明的结论解答下列问题:
设有两个非负数a、b.则有如下证明:∵($\sqrt{a}$-$\sqrt{b}$)2≥0(当且仅当a=b时等号成立).∴a-2$\sqrt{ab}$+b≥0.∴a+b≥2$\sqrt{ab}$,∴$\sqrt{ab}$≤$\frac{a+b}{2}$(或ab≤$\frac{(a+b)^{2}}{4}$)(当且仅当a=b时等号成立)根据这一证明的结论解答下列问题: