题目内容
11．小明和小刚在化简$\frac{m-n}{\sqrt{m}+\sqrt{n}}$时，给出不同的解法，小明的解法是：原式=$\frac{（\sqrt{m}+\sqrt{n}）（\sqrt{m}-\sqrt{n}）}{\sqrt{m}+\sqrt{n}}$=$\sqrt{m}$-$\sqrt{n}$；小刚的解法是：原式=$\frac{（m-n）（\sqrt{m}-\sqrt{n}）}{（\sqrt{m}+\sqrt{n}）（\sqrt{m}-\sqrt{n}）}$=$\frac{（m-n）（\sqrt{m}-\sqrt{n}）}{m-n}$=$\sqrt{m}$-$\sqrt{n}$．小红同学说他们两人结果相同，所以认为小明和小刚都是正确的，你有什么看法？谁的解法正确？分析 根据平方差公式，可得二次根式的乘除法，根据二次根式的乘除法，可得答案；
根据二次根式的乘除法，可得平方差公式，根据平方差公式，可得答案．
解答 解：小明的解法正确，原式=$\frac{（\sqrt{m}+\sqrt{n}）（\sqrt{m}-\sqrt{n}）}{\sqrt{m}+\sqrt{n}}$=$\sqrt{m}$-$\sqrt{n}$；
小刚的解法正确，原式=$\frac{（m-n）（\sqrt{m}-\sqrt{n}）}{（\sqrt{m}+\sqrt{n}）（\sqrt{m}-\sqrt{n}）}$=$\frac{（m-n）（\sqrt{m}-\sqrt{n}）}{m-n}$=$\sqrt{m}$-$\sqrt{n}$．
点评 本题考查了分母有理化，利用平方差公式、二次根式的乘法是解题关键．
练习册系列答案
相关题目
2．计算-$\frac{2}{5}$+（$\frac{5}{8}$$-\frac{1}{6}$$+\frac{7}{12}$）×（-2.4）的结果是（ ）
| A． | -2.9 | B． | 2.9 | C． | -2.8 | D． | 2.8 |
如图所示，M是梯形ABCD的腰CD的中点，MN⊥AB，垂足为N．求证：S△ABM=$\frac{1}{2}$梯形ABCD．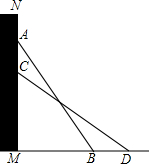
如图，把一个长为10m的梯子AB斜靠在墙上，测得AM=8m，BM=6m，梯子沿墙下滑到CD位置，测得∠ABM=∠DCM，求梯子下滑的高度．
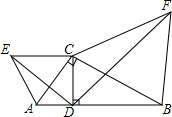如图，在Rt△ABC中，∠ACB=90°，CD⊥AB于点D，分别以AC，BC为边向三角形外作等边△ACE和等边△BCF，连接DE，DF，试说明：△ADE∽△CDF．