Question

15．如图，⊙O的直径AB与弦CD相交于点P，且有PA=5，PB=1，∠APC=60°，求弦CD的长．

Answer 1

分析 作OH⊥CD于H，连结OC，如图，先计算出直径AB=6，再得到半径为3，OP=2，接着根据垂径定理得到CH=DH，然后在Rt△OPH中，利用∠OPH的正弦计算出OH=$\sqrt{3}$，在Rt△OCH中利用勾股定理计算出CH=$\sqrt{6}$，于是得到CD=2CH=2$\sqrt{6}$．

解答 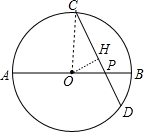解：作OH⊥CD于H，连结OC，如图，
∵PA=5，PB=1，
∴AB=PA+PB=6，
∴OB=3，OP=OB-PB=2，
∵OH⊥CD，
∴CH=DH，
在Rt△OPH中，∵sin∠OPH=$\frac{OH}{OP}$，
∴OH=2sin60°=$\sqrt{3}$，
在Rt△OCH中，∵OH=$\sqrt{3}$，OC=3，
∴CH=$\sqrt{O{C}^{2}-O{H}^{2}}$=$\sqrt{6}$，
∴CD=2CH=2$\sqrt{6}$．

点评 本题考查了垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．也考查了勾股定理．