题目内容
10．利用函数图象解不等式：2x-1≤3x-5．分析 分别令y1=2x-1，y2=3x-5，利用描点法在同一坐标系内画出两函数的图象，根据函数的图象即可解答．
解答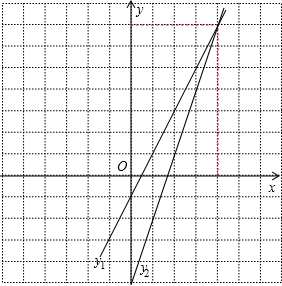 
解：令y1=2x-1，y2=3x-5，在同一坐标系内画出两函数的图象，
由图象可知，两函数的交点坐标为（4，7），
当x≥4时，y1的图象落在y2图象的下方，即2x-1≤3x-5，
所以不等式2x-1≤3x-5的解集为：x≥4．
点评 此题主要考查了一次函数与一元一次不等式，关键是正确作出函数图象，从函数的角度看，就是寻求使一次函数y=ax+b的值大于（或小于）0的自变量x的取值范围；从函数图象的角度看，就是确定直线y=kx+b在x轴上（或下）方部分所有的点的横坐标所构成的集合．
练习册系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
如图，已知直线l与⊙O相离，OA⊥l于点A，交⊙O于点P，点B是⊙O上一点，连接BP并延长，交直线l于点C，使得AB=AC．
1．下列三元一次方程组的是（ ）
| A． | $\left\{\begin{array}{l}{x+y+z=7}\\{2x+3y=5}\\{y+2x=2}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{xy=3}\\{y+z=2}\\{x+z=6}\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}{\frac{1}{x}+y+z=7}\\{2x+y+3z=5}\\{x+2y+z=2}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x+y=5}\\{3x+2y=9}\end{array}\right.$ |
如图，在四边形ABCD中，AD∥BC，AB∥DE，AF∥DC，E、F两点是边BC的三等分点，且AB=DC．求证：四边形AEFD是矩形．
如图，⊙O的直径AB与弦CD相交于点P，且有PA=5，PB=1，∠APC=60°，求弦CD的长．
19．
如图，点E在正方形ABCD的边AD上，已知AE=7，CE=13，则阴影部分的面积是（ ）
如图，点E在正方形ABCD的边AD上，已知AE=7，CE=13，则阴影部分的面积是（ ）| A． | 114 | B． | 124 | C． | 134 | D． | 144 |
20．
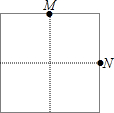在如图所示的网格中由四个相同的小正方形组成，网格图中有9个网格点，点M，N都在网格的格点上，在剩余的格点中任取一点P，使△MNP为等腰三角形的概率是（ ）
在如图所示的网格中由四个相同的小正方形组成，网格图中有9个网格点，点M，N都在网格的格点上，在剩余的格点中任取一点P，使△MNP为等腰三角形的概率是（ ）| A． | $\frac{2}{7}$ | B． | $\frac{5}{7}$ | C． | $\frac{4}{7}$ | D． | $\frac{1}{2}$ |