题目内容
7．已知方程组$\left\{\begin{array}{l}{3x+3y=m+1}\\{2x+y=m-1}\end{array}\right.$，当m为何值时，x＞y？分析 解此题首先要把字母m看做常数，然后解得x、y的值，结合题意，列得一元一次不等式，解不等式即可．
解答 解：$\left\{\begin{array}{l}{3x+3y=m+1①}\\{2x+y=m-1②}\end{array}\right.$
②×3-①得：x=$\frac{2m-4}{3}$③，
将③代入②得：y=$\frac{-m+5}{3}$，
∴$\left\{\begin{array}{l}{x=\frac{2m-4}{3}}\\{y=\frac{-m+5}{3}}\end{array}\right.$
∵x＞y，
∴$\frac{2m-4}{3}＞\frac{-m+5}{3}$，
解得：m＞3．
点评 本题考查了二元一次方程组的解，解题的关键是把字母m看做常数，然后解一元一次方程组与一元一次不等式．
练习册系列答案
相关题目
17．
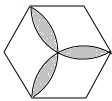向如图所示的正六边形靶子上随意抛一枚飞镖，则飞镖插在阴影区域的概率为（ ）
向如图所示的正六边形靶子上随意抛一枚飞镖，则飞镖插在阴影区域的概率为（ ）| A． | $\frac{2\sqrt{3}-π}{π}$ | B． | $\frac{2π\sqrt{3}-9}{9}$ | C． | $\frac{π-\sqrt{3}}{π}$ | D． | $\frac{π\sqrt{3}-4}{9}$ |
如图，在四边形ABCD中，AD∥BC，AB∥DE，AF∥DC，E、F两点是边BC的三等分点，且AB=DC．求证：四边形AEFD是矩形．
如图，⊙O的直径AB与弦CD相交于点P，且有PA=5，PB=1，∠APC=60°，求弦CD的长．
19．
如图，点E在正方形ABCD的边AD上，已知AE=7，CE=13，则阴影部分的面积是（ ）
如图，点E在正方形ABCD的边AD上，已知AE=7，CE=13，则阴影部分的面积是（ ）| A． | 114 | B． | 124 | C． | 134 | D． | 144 |
如图，直线y1=x+b与双曲线y2=$\frac{k}{x}$交于点A（1，4）和点B，经过点A的另一条直线与双曲线y2=$\frac{k}{x}$交于点C．则：