题目内容
5．已知关于x，y的二元一次方程组$\left\{\begin{array}{l}{2x-3y=a+6}\\{x+2y=2a-8}\end{array}\right.$的解满足x-y=a，求该方程组的解．分析 运用加减消元法解出关于x，y的二元一次方程组，把方程组的解代入x-y=a，求出a的值，代入计算得到方程组的解．
解答 解：$\left\{\begin{array}{l}{2x-3y=a+6①}\\{x+2y=2a-8②}\end{array}\right.$，
②×2-①得，
y=$\frac{3}{7}$a-$\frac{22}{7}$，
把y=$\frac{3}{7}$a-$\frac{22}{7}$代入②得，
x=$\frac{8}{7}$a-$\frac{12}{7}$，
则$\frac{8}{7}$a-$\frac{12}{7}$-（$\frac{3}{7}$a-$\frac{22}{7}$）=a，
解得，a=5
方程组的解为：$\left\{\begin{array}{l}{x=4}\\{y=-1}\end{array}\right.$．
点评 本题考查的是二元一次方程组的解法，灵活运用加减消元法解方程组是解题的关键．
练习册系列答案
培优口算题卡系列答案
开心口算题卡系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
如图，⊙O的直径AB与弦CD相交于点P，且有PA=5，PB=1，∠APC=60°，求弦CD的长．
如图，直线y1=x+b与双曲线y2=$\frac{k}{x}$交于点A（1，4）和点B，经过点A的另一条直线与双曲线y2=$\frac{k}{x}$交于点C．则：
一线段AB=10米，P点从A点出发匀速沿AB方向运动到终点B需2.5分钟，Q点从B点出发匀速沿BA方向运动到终点A需2分钟．现P、Q两点同时出发相向而行，在任一点到达终点后，两点即同时停止运动．设运动时间为x分钟．P、Q两点间的距离为y米，y与x的函数关系如图．
20．
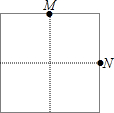在如图所示的网格中由四个相同的小正方形组成，网格图中有9个网格点，点M，N都在网格的格点上，在剩余的格点中任取一点P，使△MNP为等腰三角形的概率是（ ）
在如图所示的网格中由四个相同的小正方形组成，网格图中有9个网格点，点M，N都在网格的格点上，在剩余的格点中任取一点P，使△MNP为等腰三角形的概率是（ ）| A． | $\frac{2}{7}$ | B． | $\frac{5}{7}$ | C． | $\frac{4}{7}$ | D． | $\frac{1}{2}$ |