题目内容
已知抛物线P:y=ax2+bx+3和直线l:y=mx+n,抛物线P与x轴的两个交点分别为A(1,0)、B(x2,0),且抛物线P的对称轴为x=2,求x2的值和抛物线P的解析式.
考点:抛物线与x轴的交点
专题:计算题
分析:将A坐标代入抛物线解析式得到关系式,根据对称轴为直线x=2列出关系式,联立两关系式求出a与b的值,确定出抛物线解析式,求出x2的值即可.
解答:解:根据题意将x=1,y=0代入抛物线解析式得:a+b+3=0,①
由对称轴为直线x=2,得到-
=2,即b=-4a,②
②代入①得:-3a=-3,即a=1,
将a=1代入②得:b=-4,
则抛物线P的解析式为y=x2-4x+3,
令y=0,得到x2-4x+3=0,即(x-1)(x-3)=0,
解得:x1=1,x2=3.
由对称轴为直线x=2,得到-
| b |
| 2a |
②代入①得:-3a=-3,即a=1,
将a=1代入②得:b=-4,
则抛物线P的解析式为y=x2-4x+3,
令y=0,得到x2-4x+3=0,即(x-1)(x-3)=0,
解得:x1=1,x2=3.
点评:此题考查了抛物线与x轴交点,以及二次函数的性质,弄清题意是解本题的关键.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
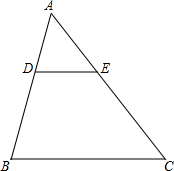 如图所示,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC,已知AD=2,DB=3,AE=3,CE=4.5,DE=4,BC=10 求证:△ADE∽△ABC.
如图所示,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC,已知AD=2,DB=3,AE=3,CE=4.5,DE=4,BC=10 求证:△ADE∽△ABC.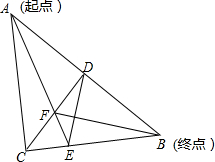 某公园内有A、B、C、D、E、F六个凉亭,连接各个凉亭的平面图形如图所示,现在我们来做一个“闯宫”的游戏,方法是:凉亭A为起点,凉亭B为终点,其中每经过一个凉亭可拿到一张纸条(每张纸条上的内容分别如下,C处:MH=M1H1;D处:MN=M1N1;E处:∠N=∠N1;F处:∠H=∠H1=90°).闯宫游戏规则是:从A点出发,中间经过三个凉亭(不分先后顺序)到达B处时,把你纸条上的三个内容综合起来恰好能说明△MNH≌△M1N1H1就算闯关成功.请你设计出三条闯宫成功的路径.
某公园内有A、B、C、D、E、F六个凉亭,连接各个凉亭的平面图形如图所示,现在我们来做一个“闯宫”的游戏,方法是:凉亭A为起点,凉亭B为终点,其中每经过一个凉亭可拿到一张纸条(每张纸条上的内容分别如下,C处:MH=M1H1;D处:MN=M1N1;E处:∠N=∠N1;F处:∠H=∠H1=90°).闯宫游戏规则是:从A点出发,中间经过三个凉亭(不分先后顺序)到达B处时,把你纸条上的三个内容综合起来恰好能说明△MNH≌△M1N1H1就算闯关成功.请你设计出三条闯宫成功的路径.
 如图,△ABC∽△DBA,∠BAC=∠ADB,写出其余的对应角和对应边的比例式.
如图,△ABC∽△DBA,∠BAC=∠ADB,写出其余的对应角和对应边的比例式.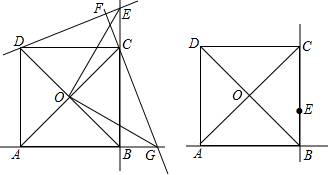
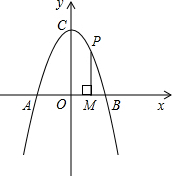 如图,抛物线y=ax2+4经过x轴上的一点A(-2,0),抛物顶点为点C,P是抛物线上的一动点.过P(不与B重合)作x轴垂线,垂足为点M,如图,若△AMC为等腰三角形,求P点的坐标.
如图,抛物线y=ax2+4经过x轴上的一点A(-2,0),抛物顶点为点C,P是抛物线上的一动点.过P(不与B重合)作x轴垂线,垂足为点M,如图,若△AMC为等腰三角形,求P点的坐标.