题目内容
4.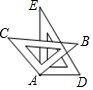 如图,将一副三角板的直角顶点重合放置于A处(两块三角板可以在同一平面内自由转动),则下列结论一定成立的是( )
如图,将一副三角板的直角顶点重合放置于A处(两块三角板可以在同一平面内自由转动),则下列结论一定成立的是( )| A. | ∠BAD≠∠EAC | B. | ∠DAC-∠BAE=45° | C. | ∠DAC+∠BAE=180° | D. | ∠DAC-∠BAE=90° |
分析 根据余角的定义、结合图形计算即可.
解答 解:∵是直角三角板,
∴∠BAC=∠DAE=90°,
∴∠BAC-∠BAE=∠DAE-∠BAE,
即∠BAD=∠EAC,①不成立;
∠DAC-∠BAE的值不固定,②不成立;
∵是直角三角板,
∴∠BAC=∠DAE=90°,
∴∠BAD+∠BAE+∠BAE+∠EAC=180°,
即∠BAE+∠DAC=180°,③成立;
∠DAC与∠BAE的大小不确定,④不成立;
故选:C.
点评 本题考查的是余角和补角的概念、角的计算,掌握余角和补角的概念、正确根据图形进行角的计算是解题的关键.

练习册系列答案
相关题目
15.下列各式属于最简二次根式的是( )
| A. | $\sqrt{8}$ | B. | $\sqrt{{a}^{2}+1}$ | C. | $\sqrt{{x}^{3}}$ | D. | $\sqrt{\frac{1}{2}}$ |
 将一副三角板如图放置,使点A在DE上,BC∥DE,则∠ACE的度数为15°.
将一副三角板如图放置,使点A在DE上,BC∥DE,则∠ACE的度数为15°.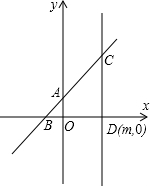 如图,经过点D(m,0)作y轴的平行线n,交一次函数y=x+1的图象于C,函数y=x+1的图象与x、y轴分别相交于B、A.(其中m>0)
如图,经过点D(m,0)作y轴的平行线n,交一次函数y=x+1的图象于C,函数y=x+1的图象与x、y轴分别相交于B、A.(其中m>0) 如图,AB∥CD,∠EAC=∠EAB,∠ECA=∠ECD,则∠AEC=90度.
如图,AB∥CD,∠EAC=∠EAB,∠ECA=∠ECD,则∠AEC=90度. 在△ABC中,作MN∥BC,且MN分别交AB,AC于点M,N两点;若AM=1,BM=3,MN=$\frac{3}{2}$,则BC的长为6.
在△ABC中,作MN∥BC,且MN分别交AB,AC于点M,N两点;若AM=1,BM=3,MN=$\frac{3}{2}$,则BC的长为6.