题目内容
15.若x2-3x+1=0.求以下代数式的值:(1)x3-x2-5x+10;
(2)x2+$\frac{1}{x^2}$.
分析 根据条件中的等式进行适当的变形,然后整体代入即可求出答案.
解答 解:∵x2-3x+1=0,
∴x2=3x-1,
(1)原式=x3-3(3x-1)-5x+10
=x3-9x+3-5x+10
=x3-8x+11
=x(x2-8)+11
=x(3x-1-8)+11
=x(3x-9)+11
=3x2-9x+11
=3(3x-1)-9x+11
=8;
(2)原式=3x-1+$\frac{1}{3x-1}$
=$\frac{(3x-1)^{2}+2}{3x-1}$
=$\frac{9{x}^{2}-6x+2}{3x-1}$
=$\frac{9(3x-1)-6x+2}{3x-1}$
=$\frac{21x-7}{3x-1}$
=7.
点评 本题考查代数式求值问题,涉及等式的变形,属于中等题型.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
3.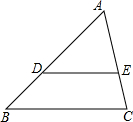 如图,DE∥BC,AD:DB=2:1,那么△ADE与△ABC的相似比为( )
如图,DE∥BC,AD:DB=2:1,那么△ADE与△ABC的相似比为( )
 如图,DE∥BC,AD:DB=2:1,那么△ADE与△ABC的相似比为( )
如图,DE∥BC,AD:DB=2:1,那么△ADE与△ABC的相似比为( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{4}$ | D. | 2 |
7. 在某一段时间里,计算机按如图所示程序工作,如果输入的数是2,那么输出的数是( )
在某一段时间里,计算机按如图所示程序工作,如果输入的数是2,那么输出的数是( )
 在某一段时间里,计算机按如图所示程序工作,如果输入的数是2,那么输出的数是( )
在某一段时间里,计算机按如图所示程序工作,如果输入的数是2,那么输出的数是( )| A. | -54 | B. | 54 | C. | -558 | D. | 558 |
5.下列关于三角形的说法错误的是( )
| A. | 三边高线的交点一定在三角形内部 | B. | 三条中线的交点在三角形内部 | ||
| C. | 三条平分线的交点在三角形内部 | D. | 以上说法均正确 |