题目内容
4.(1)解不等式:$\frac{x-2}{2}≤\frac{7-x}{3}$,并求出它的正整数解.(2)解不等式组:$\left\{\begin{array}{l}{3x+2≤2(x+3)}\\{\frac{2x-1}{3}>\frac{x}{2}}\end{array}\right.$.
分析 (1)先去分母,再去括号得到3x-6≤14-2x,接着移项、合并得5x≤20,然后把x的系数化为1得到不等式的解集,再写出解集中的正整数即可;
(2)分别解两不等式得到x≤4和x>2,然后根据大小小大中间找确定不等式组的解集.
解答 解:(1)去分母得3(x-2)≤2(7-x),
去括号得3x-6≤14-2x,
移项得3x+2x≤14+6,
合并得5x≤20,
系数化为1得x≤4,
所以不等式的正整数解为1、2、3、4;
(2)$\left\{\begin{array}{l}{3x+2≤2(x+3)①}\\{\frac{2x-1}{3}>\frac{x}{2}②}\end{array}\right.$,
解①得x≤4,
解②得x>2,
所以不等式组的解集为2<x≤4.
点评 本题考查了解一元一次不等式组:解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,利用数轴可以直观地表示不等式组的解集.解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.也考查了解一元一次不等式.

练习册系列答案
相关题目
16.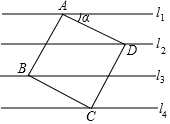 如图,已知直线l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,则sinα=( )
如图,已知直线l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,则sinα=( )
 如图,已知直线l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,则sinα=( )
如图,已知直线l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,则sinα=( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | $\frac{\sqrt{3}}{2}$ |
14.若a、b、c分别表示方程x2+1=3x中的二次项系数、一次项系数和常数项,则a、b、c的值为( )
| A. | a=1,b=-3,c=-1 | B. | a=1,b=-3,c=1 | C. | a=-1,b=-3,c=1 | D. | a=-1,b=3,c=1 |
 输入-2,按照如图所示的程序进行运算(完成一个方框内的运算后,把结果输入下一个方框继续进行运算),并写出输出的结果.
输入-2,按照如图所示的程序进行运算(完成一个方框内的运算后,把结果输入下一个方框继续进行运算),并写出输出的结果.