题目内容
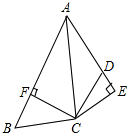 在四边形ABCD中,∠ADC+∠ABC=180°,BC=DC,CE⊥AD,交AD的延长线于点E,CF⊥AB于点F.求证:AC平分∠BAD.
在四边形ABCD中,∠ADC+∠ABC=180°,BC=DC,CE⊥AD,交AD的延长线于点E,CF⊥AB于点F.求证:AC平分∠BAD.考点:全等三角形的判定与性质,角平分线的性质
专题:证明题
分析:求出∠B=∠CDE,∠BFC=∠E=90°,证△BFC≌△DEC,推出CF=CE,根据角平分线性质得出即可.
解答:证明: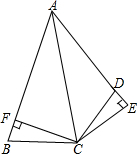
∵∠ADC+∠ABC=180°,∠ADC+∠CDE=180°,
∴∠B=∠CDE,
∵CE⊥AD,CF⊥AB,
∴∠BFC=∠E=90°,
在△BFC和△DEC中
∴△BFC≌△DEC,
∴CF=CE,
∵CE⊥AD,CF⊥AB,
∴AC平分∠BAD.

∵∠ADC+∠ABC=180°,∠ADC+∠CDE=180°,
∴∠B=∠CDE,
∵CE⊥AD,CF⊥AB,
∴∠BFC=∠E=90°,
在△BFC和△DEC中
|
∴△BFC≌△DEC,
∴CF=CE,
∵CE⊥AD,CF⊥AB,
∴AC平分∠BAD.
点评:本题考查了全等三角形的性质和判定和角平分线的性质的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
已知M(a,3)和N(4,b)关于y轴对称,则(a+b)2012的值为( )
| A、1 |
| B、-1 |
| C、72012 |
| D、-72012 |
点A(-1,-2)的位置在平面直角坐标系的( )
| A、在x轴上 | B、在y轴上 |
| C、在第三象限 | D、在第四象限 |
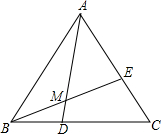 如图,D为△ABC中BC上一点,E为AC上一点,连接AD,BE交于点M,满足AM:MD=3:1,BD:DC=2:3,则AE:EC=
如图,D为△ABC中BC上一点,E为AC上一点,连接AD,BE交于点M,满足AM:MD=3:1,BD:DC=2:3,则AE:EC=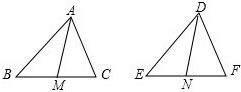 已知:△ABC和△DEF中,AB=DE,BC=EF,AM是△ABC的中线,DN是△DEF的中线,AM=DN,求证:△ABC≌△DEF.
已知:△ABC和△DEF中,AB=DE,BC=EF,AM是△ABC的中线,DN是△DEF的中线,AM=DN,求证:△ABC≌△DEF.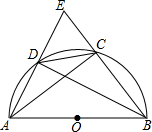 如图:AB是半圆的直径,∠ABC的平分线交半圆于D,AD和BC的延长线交于圆外一点E,连结CD.
如图:AB是半圆的直径,∠ABC的平分线交半圆于D,AD和BC的延长线交于圆外一点E,连结CD.