题目内容
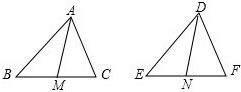 已知:△ABC和△DEF中,AB=DE,BC=EF,AM是△ABC的中线,DN是△DEF的中线,AM=DN,求证:△ABC≌△DEF.
已知:△ABC和△DEF中,AB=DE,BC=EF,AM是△ABC的中线,DN是△DEF的中线,AM=DN,求证:△ABC≌△DEF.考点:全等三角形的判定
专题:证明题
分析:求出BM=EN,根据SSS证△ABM≌△DEN,推出∠B=∠E,根据SAS推出两三角形全等即可.
解答:证明:∵BC=EF,AM是△ABC的中线,DN是△DEF的中线,
∴BM=EN,
在△ABM和△DEN中
∴△ABM≌△DEN,
∴∠B=∠E,
在△ABC和△DEF中
∴△ABC≌△DEF.
∴BM=EN,
在△ABM和△DEN中
|
∴△ABM≌△DEN,
∴∠B=∠E,
在△ABC和△DEF中
|
∴△ABC≌△DEF.
点评:本题考查了全等三角形的判定和性质的应用,全等三角形的判定定理有SAS,ASA,AAS,SSS,主要考查学生的推理能力.

练习册系列答案
相关题目
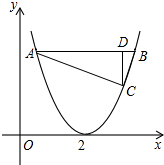 如图是二次函数y=(x-2)2的图象,点A、B、C是抛物线上3个点,且△ABC为直角三角形,CD⊥AB,则高CD应该满足( )
如图是二次函数y=(x-2)2的图象,点A、B、C是抛物线上3个点,且△ABC为直角三角形,CD⊥AB,则高CD应该满足( )| A、CD=1 |
| B、1<CD<2 |
| C、CD=2 |
| D、随着A点变化而变化 |
在同一坐标系中,作函数y=3x2,y=-3x2,y=
x2的图象,它们的共同特点是( )
| 1 |
| 3 |
| A、都是关于x轴对称,抛物线开口向上 |
| B、都是关于y轴对称,抛物线的顶点都是原点 |
| C、都是关于原点对称,抛物线的顶点都是原点 |
| D、都是关于y轴对称,抛物线开口向下 |
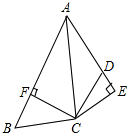 在四边形ABCD中,∠ADC+∠ABC=180°,BC=DC,CE⊥AD,交AD的延长线于点E,CF⊥AB于点F.求证:AC平分∠BAD.
在四边形ABCD中,∠ADC+∠ABC=180°,BC=DC,CE⊥AD,交AD的延长线于点E,CF⊥AB于点F.求证:AC平分∠BAD. 已知:如图,在△AOB中,A(3,2),B(5,0),E(4,m),
已知:如图,在△AOB中,A(3,2),B(5,0),E(4,m),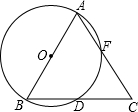 已知如图,以等腰△ABC的一腰AB为直径的⊙O交另一腰于F,交底边BC于D,探究BC与DF的关系,证明你的观点.
已知如图,以等腰△ABC的一腰AB为直径的⊙O交另一腰于F,交底边BC于D,探究BC与DF的关系,证明你的观点.