题目内容
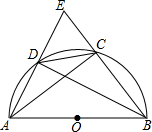 如图:AB是半圆的直径,∠ABC的平分线交半圆于D,AD和BC的延长线交于圆外一点E,连结CD.
如图:AB是半圆的直径,∠ABC的平分线交半圆于D,AD和BC的延长线交于圆外一点E,连结CD.(1)求证:△EDC是等腰三角形.
(2)若AB=5,BC=3,求四边形ABCD的面积.
考点:圆周角定理,全等三角形的判定与性质,等腰三角形的判定与性质
专题:证明题
分析:(1)根据圆周角定理由AB是半圆的直径得∠ADB=∠ACB=90°,加上∠ABC的平分线交半圆于D,根据等腰三角形的判定得BA=BE,再根据等腰三角形的性质得AD=ED,即可得到CD为直角三角形ACE斜边上的中线,所以CD=DE=AD,因此可判断△EDC是等腰三角形;
(2)先利用BA=BE=5得到CE=EB-CB=2,利用勾股定理,在Rt△ACE中计算出AE=2
,在Rt△ABC中计算出AC=4,利用三角形面积公式得到S△ABE=
AC•BE=10,再证明△ECD∽△EAB,利用相似的性质求出S△ECD=2,然后利用四边形ABCD的面积=S△ABE-S△ECD进行计算..
(2)先利用BA=BE=5得到CE=EB-CB=2,利用勾股定理,在Rt△ACE中计算出AE=2
| 5 |
| 1 |
| 2 |
解答:(1)证明:∵AB是半圆的直径,
∴∠ADB=∠ACB=90°,
∵∠ABC的平分线交半圆于D,
∴BA=BE,
∴AD=ED,
∴CD为直角三角形ACE斜边上的中线,
∴CD=DE=AD,
∴△EDC是等腰三角形;
(2)解:∵BA=BE=5,
∴CE=EB-CB=2,
在Rt△ACE中,AE=
=2
,
在Rt△ABC中,AC=
=4,
∴S△ABE=
AC•BE=
×4×5=10,
∵∠EDC=∠EBA,
而∠DEC=∠BEA,
∴△ECD∽△EAB,
∴
=(
)2,即S△ECD=10×(
)2=2,
∴四边形ABCD的面积=S△ABE-S△ECD=10-2=8.
∴∠ADB=∠ACB=90°,
∵∠ABC的平分线交半圆于D,
∴BA=BE,
∴AD=ED,
∴CD为直角三角形ACE斜边上的中线,
∴CD=DE=AD,
∴△EDC是等腰三角形;
(2)解:∵BA=BE=5,
∴CE=EB-CB=2,
在Rt△ACE中,AE=
| AC2+CE2 |
| 5 |
在Rt△ABC中,AC=
| AB2-BC2 |
∴S△ABE=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠EDC=∠EBA,
而∠DEC=∠BEA,
∴△ECD∽△EAB,
∴
| S△ECD |
| S△EAB |
| EC |
| EA |
| 2 | ||
2
|
∴四边形ABCD的面积=S△ABE-S△ECD=10-2=8.
点评:本题考查了圆周角定理:圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了等腰三角形的判定与性质和相似三角形的判定与性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在同一坐标系中,作函数y=3x2,y=-3x2,y=
x2的图象,它们的共同特点是( )
| 1 |
| 3 |
| A、都是关于x轴对称,抛物线开口向上 |
| B、都是关于y轴对称,抛物线的顶点都是原点 |
| C、都是关于原点对称,抛物线的顶点都是原点 |
| D、都是关于y轴对称,抛物线开口向下 |
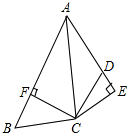 在四边形ABCD中,∠ADC+∠ABC=180°,BC=DC,CE⊥AD,交AD的延长线于点E,CF⊥AB于点F.求证:AC平分∠BAD.
在四边形ABCD中,∠ADC+∠ABC=180°,BC=DC,CE⊥AD,交AD的延长线于点E,CF⊥AB于点F.求证:AC平分∠BAD.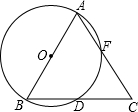 已知如图,以等腰△ABC的一腰AB为直径的⊙O交另一腰于F,交底边BC于D,探究BC与DF的关系,证明你的观点.
已知如图,以等腰△ABC的一腰AB为直径的⊙O交另一腰于F,交底边BC于D,探究BC与DF的关系,证明你的观点.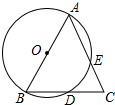 在△ABC中,AB=AC,以AB为直径的圆O分别交BC、AC于点D、E,
在△ABC中,AB=AC,以AB为直径的圆O分别交BC、AC于点D、E,