题目内容
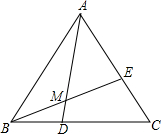 如图,D为△ABC中BC上一点,E为AC上一点,连接AD,BE交于点M,满足AM:MD=3:1,BD:DC=2:3,则AE:EC=
如图,D为△ABC中BC上一点,E为AC上一点,连接AD,BE交于点M,满足AM:MD=3:1,BD:DC=2:3,则AE:EC=考点:平行线分线段成比例
专题:
分析:过点D作DG∥AC交BE于点G,用平行线分线段成比例定理以及比例的性质进行变形即可得到答案.
解答: 解:如图,过点D作DG∥AC交BE于点G.
解:如图,过点D作DG∥AC交BE于点G.
∵DG∥AC,
∴
=
=
,
=
=
=
,
∴
=
=
=
.
故答案为
.
 解:如图,过点D作DG∥AC交BE于点G.
解:如图,过点D作DG∥AC交BE于点G.∵DG∥AC,
∴
| DG |
| CE |
| BD |
| BC |
| 2 |
| 5 |
| DG |
| AE |
| DM |
| AM |
| 1 |
| 3 |
| 2 |
| 6 |
∴
| AE |
| EC |
| ||
|
| ||
|
| 6 |
| 5 |
故答案为
| 6 |
| 5 |
点评:此题主要考查平行线分线段成比例定理,用到的知识点:平行于三角形的一边,并且和其他两边(或两边的延长线)相交的直线,所截得的三角形的三边与原三角形的三边对应成比例.准确作出辅助线是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
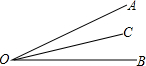 如图,下列结论中,不能说明射线OC平分∠AOB的是( )
如图,下列结论中,不能说明射线OC平分∠AOB的是( )| A、∠AOC=∠BOC |
| B、∠AOB=2∠BOC |
| C、∠AOB=2∠BOC |
| D、∠AOC+∠BOC=∠BOA |
点A,B,P在同一直线上,下列说法正确的是( )
| A、若AB=2PA,则P是AB的中点 |
| B、若AB=PB,则P是AB的中点 |
| C、若AB=2PB,则P是AB的中点 |
| D、若AB=2PA=2PB,则P是AB的中点 |
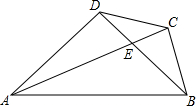 如图,在四边形ABCD中,AC与BD相交于点E,AD=BD,∠ADB=∠ACB=90°,AE=2BC.
如图,在四边形ABCD中,AC与BD相交于点E,AD=BD,∠ADB=∠ACB=90°,AE=2BC.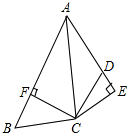 在四边形ABCD中,∠ADC+∠ABC=180°,BC=DC,CE⊥AD,交AD的延长线于点E,CF⊥AB于点F.求证:AC平分∠BAD.
在四边形ABCD中,∠ADC+∠ABC=180°,BC=DC,CE⊥AD,交AD的延长线于点E,CF⊥AB于点F.求证:AC平分∠BAD. 在△ABC中,AB=AC,以AB为直径的圆O分别交BC、AC于点D、E,
在△ABC中,AB=AC,以AB为直径的圆O分别交BC、AC于点D、E,