题目内容

2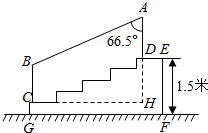．如图，某城市市民广场一入口处有五级高度相等的小台阶．已知台阶总高1.5米，为了安全，现要做一个不锈钢扶手AB及两根与FG垂直且长为1米的不锈钢架杆AD和BC（杆子的底端分别为D、C），且∠DAB=66.5°．（参考数据：cos66.5°≈0.40，sin66.5°≈0.92）
（1）求点D与点C的高度差DH；
（2）求所有不锈钢材料的总长度（即AD+AB+BC的长，结果精确到0.1米）

分析 （1）根据图形求出即可；
（2）过B作BM⊥AD于M，先求出AM，再解直角三角形求出即可．

解答 解：（1）DH=1.5米×$\frac{4}{5}$=1.2米；

（2）过B作BM⊥AD于M，

在矩形BCHM中，MH=BC=1米，
AM=AD+DH-MH=1米+1.2米-1米=1.2米，
在Rt△AMB中，AB=$\frac{AM}{cos66.5°}$≈3.00米，
所以不锈钢材料的总长度为1米+3.00米+1米=5.0米．

点评 本题考查了解直角三角形和锐角三角函数的定义的应用，能熟记锐角三角函数的定义是解此题的关键．

练习册系列答案
相关题目
12．猜想：如图①，在?ABCD中，点O是对角线AC的中点，过点O的直线分别交AD、BC于点E、F．若?ABCD的面积是10，则四边形CDEF的面积是5．
探究：如图②，在菱形ABCD中，对角线AC、BD相交于点O，过点O的直线分别交AD、BC于点E、F．若AC=4，BD=8，求四边形ABFE的面积．
应用：如图③，在Rt△ABC中，∠BAC=90°，延长BC到点D，使DC=BC，连结AD．若AC=4，$AD=\sqrt{73}$，则△ABD的面积是12．
13．如图，四边形ABCD内接于⊙O，F是$\widehat{CD}$上一点，且$\widehat{DF}$=$\widehat{BC}$，连接CF并延长交AD的延长线于点E，连接AC．若∠ABC=105°，∠BAC=25°，则∠E的度数为（　　）
A．45°B．50°C．55°D．60°
10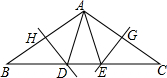．如图，在△ABC中，∠B=∠C=36°，AB的垂直平分线交BC于点D，交AB于点H，AC的垂直平分线交BC于点E，交AC于点G，连接AD，AE，则下列结论错误的是（　　）
A．$\frac{BD}{BC}$=$\frac{\sqrt{5}-1}{2}$B．AD，AE将∠BAC三等分
C．△ABE≌△ACDD．S△ADH=S△CEG
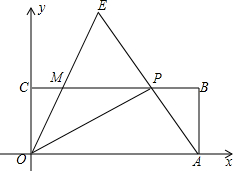17．如图，在直角坐标系xOy中，矩形OABC的顶点A、C分别在x轴和y轴正半轴上，点B的坐标是（5，2），点P是CB边上一动点（不与点C、点B重合），连结OP、AP，过点O作射线OE交AP的延长线于点E，交CB边于点M，且∠AOP=∠COM，令CP=x，MP=y．
（1）当x为何值时，OP⊥AP？
（2）求y与x的函数关系式，并写出x的取值范围；
（3）在点P的运动过程中，是否存在x，使△OCM的面积与△ABP的面积之和等于△EMP的面积？若存在，请求x的值；若不存在，请说明理由．
7．已知正方形ABCD，P为射线AB上的一点，以BP为边作正方形BPEF，使点F在线段CB的延长线上，连接EA、EC．

（1）如图1，若点P在线段AB的延长线上，求证：EA=EC；
（2）若点P在线段AB上．
①如图2，连接AC，当P为AB的中点时，判断△ACE的形状，并说明理由；
②如图3，设AB=a，BP=b，当EP平分∠AEC时，求a：b及∠AEC的度数．
14．小明、小刚和小红打算各自随机选择本周日的上午或下午去扬州马可波罗花世界游玩．
（1）小明和小刚都在本周日上午去游玩的概率为$\frac{1}{4}$；
（2）求他们三人在同一个半天去游玩的概率．
11．据统计，2015年广州地铁日均客运量均为6 590 000人次，将6 590 000用科学记数法表示为（　　）
A．6.59×104B．659×104C．65.9×105D．6.59×106
12．当x=2时，分式$\frac{x-2}{2x+5}$的值为0．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网