题目内容
5.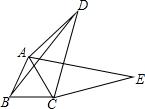 如图,四边形ABCD中,AC,BD是对角线,△ABC是等边三角形.线段CD绕点C顺时针旋转60°得到线段CE,连接AE.
如图,四边形ABCD中,AC,BD是对角线,△ABC是等边三角形.线段CD绕点C顺时针旋转60°得到线段CE,连接AE.(1)求证:AE=BD;
(2)若∠ADC=30°,AD=3,BD=4$\sqrt{2}$.求CD的长.
分析 (1)根据AC=BC、∠DCE+∠ACD=∠ACB+∠ACD、CE=CD证△ACE≌△BCD即可;
(2)连接DE,可得△DCE是等边三角形,即∠CDE=60°、DC=DE,继而在RT△ADE中,由勾股定理可得DE的长,即可知CD.
解答 解:(1)∵△ABC是等边三角形,
∴AC=BC,∠ACB=60°.
由旋转的性质可得:
CE=CD,∠DCE=60°.
∴∠DCE+∠ACD=∠ACB+∠ACD,
即∠ACE=∠BCD.
在△ACE≌△BCD中,
∵$\left\{\begin{array}{l}{AC=BC}\\{∠ACE=∠BCD}\\{CD=CE}\end{array}\right.$,
∴△ACE≌△BCD.
∴AE=BD.
(2)连接DE.
∵CD=CE,∠DCE=60°,
∴△DCE是等边三角形.
∴∠CDE=60°,DC=DE.
∵∠ADC=30°,
∴∠ADC+∠CDE=90°.
∵AD=3,BD=4$\sqrt{2}$,
∴AE=BD=4$\sqrt{2}$.
在Rt△ADE中,由勾股定理,
可得DE=$\sqrt{A{E}^{2}-A{D}^{2}}$=$\sqrt{(4\sqrt{2})^{2}-{3}^{2}}$=$\sqrt{23}$.
∴DC=DE=$\sqrt{23}$.
点评 本题主要考查旋转的性质、全等三角形的判定与性质及勾股定理的应用,连接DE发现等边三角形与直角三角形是解题的关键.

练习册系列答案
相关题目
15. 某校以“我最喜爱的体育运动”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
某校以“我最喜爱的体育运动”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
请根据以上图表信息解答下列问题:
(1)频数分布表中的m=24,n=0.30;
(2)在扇形统计图中,“乒乓球”所在的扇形的圆心角的度数为108;
(3)根据统计数据估计该校1200名中学生中,最喜爱乒乓球这项运动的约有360人.
 某校以“我最喜爱的体育运动”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
某校以“我最喜爱的体育运动”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:| 运动项目 | 频数(人数) | 频率 |
| 篮球 | 30 | 0.25 |
| 羽毛球 | m | 0.20 |
| 乒乓球 | 36 | n |
| 跳绳 | 18 | 0.15 |
| 其它 | 1 | 0.10 |
(1)频数分布表中的m=24,n=0.30;
(2)在扇形统计图中,“乒乓球”所在的扇形的圆心角的度数为108;
(3)根据统计数据估计该校1200名中学生中,最喜爱乒乓球这项运动的约有360人.
16.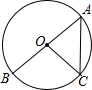 如图,AB为⊙O的直径,点C在⊙O上,若∠OCA=50°,AB=4,则$\widehat{BC}$的长为( )
如图,AB为⊙O的直径,点C在⊙O上,若∠OCA=50°,AB=4,则$\widehat{BC}$的长为( )
 如图,AB为⊙O的直径,点C在⊙O上,若∠OCA=50°,AB=4,则$\widehat{BC}$的长为( )
如图,AB为⊙O的直径,点C在⊙O上,若∠OCA=50°,AB=4,则$\widehat{BC}$的长为( )| A. | $\frac{10}{3}$π | B. | $\frac{10}{9}$π | C. | $\frac{5}{9}$π | D. | $\frac{5}{18}$π |
13. 如图,四边形ABCD内接于⊙O,F是$\widehat{CD}$上一点,且$\widehat{DF}$=$\widehat{BC}$,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=25°,则∠E的度数为( )
如图,四边形ABCD内接于⊙O,F是$\widehat{CD}$上一点,且$\widehat{DF}$=$\widehat{BC}$,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=25°,则∠E的度数为( )
 如图,四边形ABCD内接于⊙O,F是$\widehat{CD}$上一点,且$\widehat{DF}$=$\widehat{BC}$,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=25°,则∠E的度数为( )
如图,四边形ABCD内接于⊙O,F是$\widehat{CD}$上一点,且$\widehat{DF}$=$\widehat{BC}$,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=25°,则∠E的度数为( )| A. | 45° | B. | 50° | C. | 55° | D. | 60° |
20. 如图,直线a∥b,直线l分别与直线a,b相交于点P,Q,PM垂直于l,若∠1=58°,则∠2的度数为( )
如图,直线a∥b,直线l分别与直线a,b相交于点P,Q,PM垂直于l,若∠1=58°,则∠2的度数为( )
 如图,直线a∥b,直线l分别与直线a,b相交于点P,Q,PM垂直于l,若∠1=58°,则∠2的度数为( )
如图,直线a∥b,直线l分别与直线a,b相交于点P,Q,PM垂直于l,若∠1=58°,则∠2的度数为( )| A. | 58° | B. | 90° | C. | 32° | D. | 38° |
10.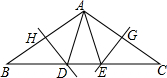 如图,在△ABC中,∠B=∠C=36°,AB的垂直平分线交BC于点D,交AB于点H,AC的垂直平分线交BC于点E,交AC于点G,连接AD,AE,则下列结论错误的是( )
如图,在△ABC中,∠B=∠C=36°,AB的垂直平分线交BC于点D,交AB于点H,AC的垂直平分线交BC于点E,交AC于点G,连接AD,AE,则下列结论错误的是( )
 如图,在△ABC中,∠B=∠C=36°,AB的垂直平分线交BC于点D,交AB于点H,AC的垂直平分线交BC于点E,交AC于点G,连接AD,AE,则下列结论错误的是( )
如图,在△ABC中,∠B=∠C=36°,AB的垂直平分线交BC于点D,交AB于点H,AC的垂直平分线交BC于点E,交AC于点G,连接AD,AE,则下列结论错误的是( )| A. | $\frac{BD}{BC}$=$\frac{\sqrt{5}-1}{2}$ | B. | AD,AE将∠BAC三等分 | ||
| C. | △ABE≌△ACD | D. | S△ADH=S△CEG |
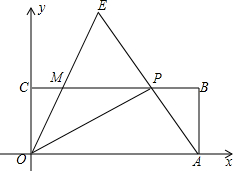 如图,在直角坐标系xOy中,矩形OABC的顶点A、C分别在x轴和y轴正半轴上,点B的坐标是(5,2),点P是CB边上一动点(不与点C、点B重合),连结OP、AP,过点O作射线OE交AP的延长线于点E,交CB边于点M,且∠AOP=∠COM,令CP=x,MP=y.
如图,在直角坐标系xOy中,矩形OABC的顶点A、C分别在x轴和y轴正半轴上,点B的坐标是(5,2),点P是CB边上一动点(不与点C、点B重合),连结OP、AP,过点O作射线OE交AP的延长线于点E,交CB边于点M,且∠AOP=∠COM,令CP=x,MP=y. 如图,在平面直角坐标系中,二次函数y=-$\frac{1}{4}$x2+bx+c的图象与坐标轴交于A、B、C三点,其中点A的坐标为(0,8),点B的坐标为(-4,0).
如图,在平面直角坐标系中,二次函数y=-$\frac{1}{4}$x2+bx+c的图象与坐标轴交于A、B、C三点,其中点A的坐标为(0,8),点B的坐标为(-4,0).