题目内容
4．菱形的两条对角线长分别为6和8，则菱形的周长是（ ）| A． | 40 | B． | 24 | C． | 20 | D． | 10 |
分析 根据菱形的对角线互相垂直平分的性质，利用对角线的一半，根据勾股定理求出菱形的边长，再根据菱形的四条边相等求出周长即可．
解答 解：如图所示，
∵四边形ABCD是菱形，
∴AO=$\frac{1}{2}$×8=4，BO=$\frac{1}{2}$×6=3，AB=BC=CD=DA，AC⊥BD，
∴△AOB是直角三角形，
∴AB=$\sqrt{A{O}^{2}+B{O}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5，
∴此菱形的周长=5×4=20．
故选：C．
点评 本题主要考查了菱形的性质，勾股定理；熟练掌握菱形的性质，由勾股定理求出边长是解题的关键
练习册系列答案
相关题目
15．
某校以“我最喜爱的体育运动”为主题对全校学生进行随机抽样调查，调查的运动项目有：篮球、羽毛球、乒乓球、跳绳及其它项目（每位同学仅选一项）．根据调查结果绘制了如下不完整的频数分布表和扇形统计图：
请根据以上图表信息解答下列问题：
（1）频数分布表中的m=24，n=0.30；
（2）在扇形统计图中，“乒乓球”所在的扇形的圆心角的度数为108；
（3）根据统计数据估计该校1200名中学生中，最喜爱乒乓球这项运动的约有360人．
某校以“我最喜爱的体育运动”为主题对全校学生进行随机抽样调查，调查的运动项目有：篮球、羽毛球、乒乓球、跳绳及其它项目（每位同学仅选一项）．根据调查结果绘制了如下不完整的频数分布表和扇形统计图：| 运动项目 | 频数（人数） | 频率 |
| 篮球 | 30 | 0.25 |
| 羽毛球 | m | 0.20 |
| 乒乓球 | 36 | n |
| 跳绳 | 18 | 0.15 |
| 其它 | 1 | 0.10 |
（1）频数分布表中的m=24，n=0.30；
（2）在扇形统计图中，“乒乓球”所在的扇形的圆心角的度数为108；
（3）根据统计数据估计该校1200名中学生中，最喜爱乒乓球这项运动的约有360人．
19．
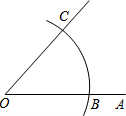如图，以O为圆心，任意长为半径画弧，与射线OA交于点B，再以B为圆心，BO长为半径画弧，两弧交于点C，画射线OC，则sin∠AOC的值为（ ）
如图，以O为圆心，任意长为半径画弧，与射线OA交于点B，再以B为圆心，BO长为半径画弧，两弧交于点C，画射线OC，则sin∠AOC的值为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{3}}{3}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | $\frac{\sqrt{3}}{2}$ |
9．算式2.5÷[（$\frac{1}{5}$-1）×（2+$\frac{1}{2}$）]之值为何？（ ）
| A． | -$\frac{5}{4}$ | B． | -$\frac{125}{16}$ | C． | -25 | D． | 11 |
16．
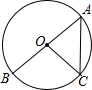如图，AB为⊙O的直径，点C在⊙O上，若∠OCA=50°，AB=4，则$\widehat{BC}$的长为（ ）
如图，AB为⊙O的直径，点C在⊙O上，若∠OCA=50°，AB=4，则$\widehat{BC}$的长为（ ）| A． | $\frac{10}{3}$π | B． | $\frac{10}{9}$π | C． | $\frac{5}{9}$π | D． | $\frac{5}{18}$π |
如图，四边形ABCD内接于⊙O，F是$\widehat{CD}$上一点，且$\widehat{DF}$=$\widehat{BC}$，连接CF并延长交AD的延长线于点E，连接AC．若∠ABC=105°，∠BAC=25°，则∠E的度数为（ ）