题目内容
18．已知，一元二次方程x2-8x+15=0的两根分别是⊙O1和⊙O2的半径，当⊙O1和⊙O2相切时，O1O2的长度是（ ）| A． | 2 | B． | 8 | C． | 2或8 | D． | 2＜O1O2＜8 |
分析 先解方程求出⊙O1、⊙O2的半径，再分两圆外切和两圆内切两种情况讨论求解．
解答 解：∵⊙O1、⊙O2的半径分别是方程x2-8x+15=0的两根，
解得⊙O1、⊙O2的半径分别是3和5．
∴①当两圆外切时，圆心距O1O2=3+5=8；
②当两圆内切时，圆心距O1O2=5-3=2．
故选C．
点评 考查解一元二次方程-因式分解法和圆与圆的位置关系，同时考查综合应用能力及推理能力．注意：两圆相切，应考虑内切或外切两种情况是解本题的难点．
练习册系列答案
相关题目
9．算式2.5÷[（$\frac{1}{5}$-1）×（2+$\frac{1}{2}$）]之值为何？（ ）
| A． | -$\frac{5}{4}$ | B． | -$\frac{125}{16}$ | C． | -25 | D． | 11 |
6．下列计算正确的是（ ）
| A． | 3a2-6a2=-3 | B． | （-2a）•（-a）=2a2 | C． | 10a10÷2a2=5a5 | D． | -（a3）2=a6 |
13．
如图，四边形ABCD内接于⊙O，F是$\widehat{CD}$上一点，且$\widehat{DF}$=$\widehat{BC}$，连接CF并延长交AD的延长线于点E，连接AC．若∠ABC=105°，∠BAC=25°，则∠E的度数为（ ）
如图，四边形ABCD内接于⊙O，F是$\widehat{CD}$上一点，且$\widehat{DF}$=$\widehat{BC}$，连接CF并延长交AD的延长线于点E，连接AC．若∠ABC=105°，∠BAC=25°，则∠E的度数为（ ）| A． | 45° | B． | 50° | C． | 55° | D． | 60° |
3．
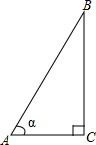如图，为测量一棵与地面垂直的树BC的高度，在距离树的底端4米的A处，测得树顶B的仰角∠α=74°，则树BC的高度为（ ）
如图，为测量一棵与地面垂直的树BC的高度，在距离树的底端4米的A处，测得树顶B的仰角∠α=74°，则树BC的高度为（ ）| A． | $\frac{4}{tan74°}$米 | B． | 4sin74°米 | C． | 4tan74°米 | D． | 4cos74°米 |
10．
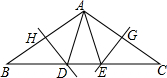如图，在△ABC中，∠B=∠C=36°，AB的垂直平分线交BC于点D，交AB于点H，AC的垂直平分线交BC于点E，交AC于点G，连接AD，AE，则下列结论错误的是（ ）
如图，在△ABC中，∠B=∠C=36°，AB的垂直平分线交BC于点D，交AB于点H，AC的垂直平分线交BC于点E，交AC于点G，连接AD，AE，则下列结论错误的是（ ）| A． | $\frac{BD}{BC}$=$\frac{\sqrt{5}-1}{2}$ | B． | AD，AE将∠BAC三等分 | ||
| C． | △ABE≌△ACD | D． | S△ADH=S△CEG |
