题目内容
18.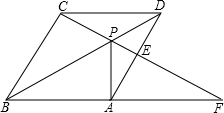 如图,点P是菱形ABCD对角线BD上一点,连结CP并延长,交AD于E,交BA的延长线于F,
如图,点P是菱形ABCD对角线BD上一点,连结CP并延长,交AD于E,交BA的延长线于F,(1)求证:∠BCP=∠BAP;
(2)若AB=3,DP:PB=1:3,且PA⊥BF,求PA和BD的长.
分析 (1)直接利用菱形的性质结合全等三角形的判定方法得出:∠BCP=∠BAP;
(2)直接利用已知得出△CDP∽△FBP,可得BF的长,再利用勾股定理得出答案.
解答 (1)证明:∵四边形ABCD是菱形,
∴∠CBD=∠ABD,BC=AB,
在△CBD和△ABD中,
$\left\{\begin{array}{l}{BC=BA}\\{∠CBD=∠ABD}\\{BP=BP}\end{array}\right.$,
∴△CBD≌△ABD(SAS),
∴∠BCP=∠BAP;
(2)解:∵AB=3,
∴CD=3,
∵DC∥AB,
∴△CDP∽△FBP,
∴$\frac{DC}{BF}$=$\frac{DP}{BP}$=$\frac{CP}{PF}$=$\frac{1}{3}$,
∴BF=3CD=9,
∴AF=6,
∵PA⊥BF,
∴BC⊥CF,
∴Rt△BCF中,
CF=$\sqrt{B{F}^{2}-B{C}^{2}}$=6$\sqrt{2}$,
∴PF=$\frac{3}{4}$CF=$\frac{9\sqrt{2}}{2}$,
∴Rt△PAF中,PA=$\sqrt{P{F}^{2}-A{F}^{2}}$=$\frac{\sqrt{2}}{2}$×3=$\frac{3\sqrt{2}}{2}$,
∴Rt△ABP中,BP=$\sqrt{A{B}^{2}+A{P}^{2}}$=$\frac{\sqrt{6}}{2}$×3=$\frac{3\sqrt{6}}{2}$,
∴BD=$\frac{4}{3}$BP=$\frac{2\sqrt{6}}{3}$×3=2$\sqrt{6}$.
点评 此题主要考查了菱形的性质以及全等三角形的判定与性质和勾股定理等知识,正确应用菱形的性质是解题关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
8.下列说法中,正确的是( )
①四边形在平移过程中,对应线段一定相等;②四边形在平移过程中,对应线段一定平行;③四边形在平移过程中,周长不变;④四边形在平移过程中,面积不变.
①四边形在平移过程中,对应线段一定相等;②四边形在平移过程中,对应线段一定平行;③四边形在平移过程中,周长不变;④四边形在平移过程中,面积不变.
| A. | ①②③ | B. | ①②③④ | C. | ②③④ | D. | ①③④ |
13. 将一副三角板如图放置,使点D落在AB上,如果EC∥AB,那么∠DFC的度数为( )
将一副三角板如图放置,使点D落在AB上,如果EC∥AB,那么∠DFC的度数为( )
 将一副三角板如图放置,使点D落在AB上,如果EC∥AB,那么∠DFC的度数为( )
将一副三角板如图放置,使点D落在AB上,如果EC∥AB,那么∠DFC的度数为( )| A. | 45° | B. | 50° | C. | 60° | D. | 75° |
 如图,直线a∥b,BC平分∠ABD,DE⊥BC,若∠1=70°,求∠2的度数.
如图,直线a∥b,BC平分∠ABD,DE⊥BC,若∠1=70°,求∠2的度数.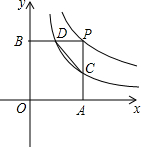 如图,点P是双曲线y=$\frac{6}{x}$右支上一动点.PA⊥x轴于点A,PB⊥y轴于点B,D是PB的中点
如图,点P是双曲线y=$\frac{6}{x}$右支上一动点.PA⊥x轴于点A,PB⊥y轴于点B,D是PB的中点 已知:如图,在△ABC中,以AB为直径的⊙O分别交AC、BC于点D、E,且AD=DC.
已知:如图,在△ABC中,以AB为直径的⊙O分别交AC、BC于点D、E,且AD=DC.