题目内容
6.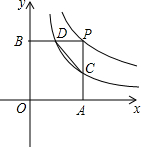 如图,点P是双曲线y=$\frac{6}{x}$右支上一动点.PA⊥x轴于点A,PB⊥y轴于点B,D是PB的中点
如图,点P是双曲线y=$\frac{6}{x}$右支上一动点.PA⊥x轴于点A,PB⊥y轴于点B,D是PB的中点(1)求过点D的双曲线的表达式;
(2)若过点D的双曲线与PA交于点C,请求出△PDC的面积.
分析 (1)设过点D的双曲线解析式为:y=$\frac{k}{x}$,点D的坐标为(a,$\frac{k}{a}$),由D是PB的中点可得点P的坐标为(2a,$\frac{k}{a}$),代入y=$\frac{6}{x}$得k的值;
(2)过点D作DE⊥OA于点E,由(1)知点D坐标为(a,$\frac{3}{a}$)、点D(2a,$\frac{3}{a}$)、点C(2a,$\frac{3}{2a}$),继而分别表示出AC、DE、AE的长,根据S△PDC=S矩形OAPB-S矩形OEDB-S梯形ACDE可得答案.
解答 解:(1)设过点D的双曲线解析式为:y=$\frac{k}{x}$,点D的坐标为(a,$\frac{k}{a}$),
∵PA⊥x轴于点A,PB⊥y轴于点B,D是PB的中点,
∴点P的坐标为(2a,$\frac{k}{a}$),
将点P坐标代入y=$\frac{6}{x}$得:$\frac{k}{a}=\frac{6}{2a}$,
解得:k=3,
故过点D的双曲线的表达式为y=$\frac{3}{x}$;
(2)过点D作DE⊥OA于点E,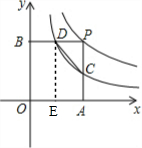
由(1)可知点D坐标为(a,$\frac{3}{a}$)、点D(2a,$\frac{3}{a}$)、点C(2a,$\frac{3}{2a}$),
∴AC=$\frac{3}{2a}$,DE=$\frac{3}{a}$,AE=a,
∴S△PDC=S矩形OAPB-S矩形OEDB-S梯形ACDE
=6-3-$\frac{1}{2}$×a×($\frac{3}{2a}$+$\frac{3}{a}$)
=$\frac{3}{4}$.
点评 本题考查了反比例函数性质的综合运用,涉及点的坐标转化,三角形、四边形面积的计算,充分运用双曲线上点的横坐标与纵坐标的积等于反比例系数k.

 阅读快车系列答案
阅读快车系列答案| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
 如图,△ABC内接于⊙O,AB=8,BC=10,AC=6,D是弧AB的中点,连接CD交AB于点E,则DE:CE等于( )
如图,△ABC内接于⊙O,AB=8,BC=10,AC=6,D是弧AB的中点,连接CD交AB于点E,则DE:CE等于( )| A. | 2:5 | B. | 1:3 | C. | 2:7 | D. | 1:4 |
| A. | 64的立方根是±4 | B. | -$\frac{27}{64}$的立方根是$\frac{3}{4}$ | ||
| C. | -2是-8的立方根 | D. | -125的立方根是±5 |
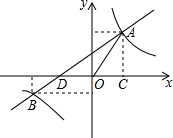 如图,在平面直角坐标系中,双曲线y=$\frac{m}{x}$与直线y=kx+b相交于A、B两点,过点A作AC⊥x轴于点C,其中AC=4,tan∠AOC=$\frac{4}{3}$且点B的坐标为(-6,n).
如图,在平面直角坐标系中,双曲线y=$\frac{m}{x}$与直线y=kx+b相交于A、B两点,过点A作AC⊥x轴于点C,其中AC=4,tan∠AOC=$\frac{4}{3}$且点B的坐标为(-6,n). 已知:如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点M,交BC于点N,且AM=BC,点P是AB延长线上的一点,∠PCB=$\frac{1}{2}$∠BAC.
已知:如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点M,交BC于点N,且AM=BC,点P是AB延长线上的一点,∠PCB=$\frac{1}{2}$∠BAC.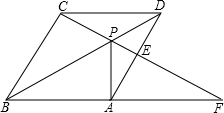 如图,点P是菱形ABCD对角线BD上一点,连结CP并延长,交AD于E,交BA的延长线于F,
如图,点P是菱形ABCD对角线BD上一点,连结CP并延长,交AD于E,交BA的延长线于F,